Для метода Лагранжа значение n+1=5, то есть порядок интерполяционного полинома n=4.
В общем случае интерполяционный полином Лагранжа представляется как:
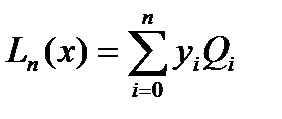
где: y i – значение исходной таблицы данных.
Q i – вспомогательные функции.
Для нашего случая полином 4-го порядка равен:
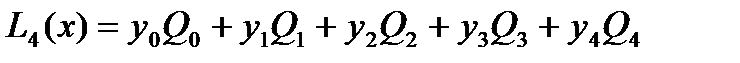
1.2.4 Определение вспомогательных функций Qi(x)
Вспомогательные функции Qi(x) определяются как
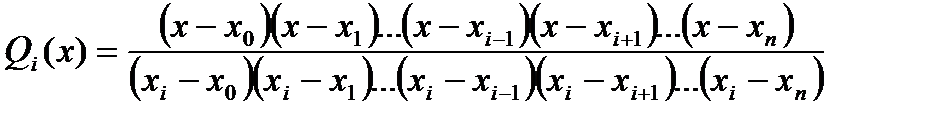
Для нашего полинома вспомогательные функции будут следующими:
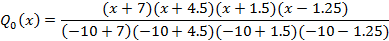
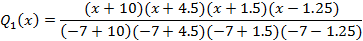
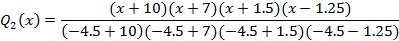
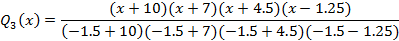
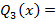
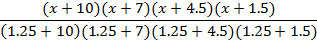
1.2.5 Определение интерполяционного полинома
Подставляя вспомогательные функции и значения ординат узлов интерполяции получаем необходимую интерполяционную функцию.
L 4(x) = y0  + y1
+ y1 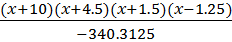 +
+
+ y2 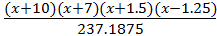 + y3
+ y3 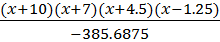 +
+
+ y4 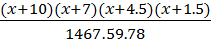
Восстановление исходной функции в заданной точке, при помощи интерполяционного полинома
Примем точку, в которой будем восстанавливать исходную функцию за x = -2.
L 4(-2) = -14.121  + +4.206
+ +4.206 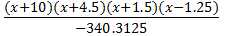 - 0.99
- 0.99 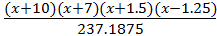 -
-
6.294 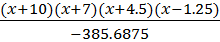 +9.031
+9.031 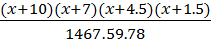
L 4(-2) = -5.66335
1.2.7 Определение погрешности интерполяции путем сравнения значения х, полученного по интерполяционному полиному, и рассчитанного по f(x)
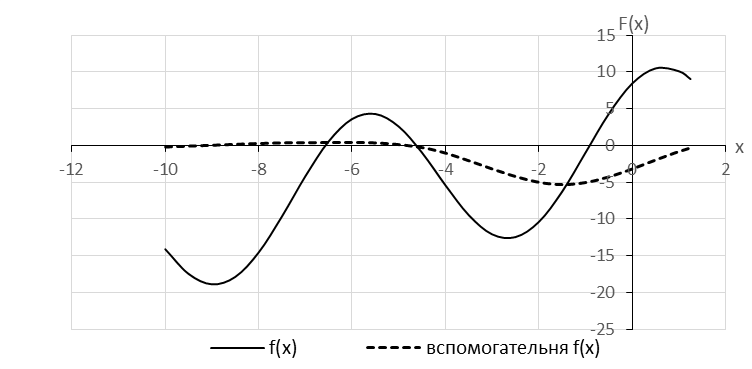
Рис.1 - Определение интерполяционного полинома Лагранжа
f (-2) = -2 +10sin(-2+1) = -10.4147
Для оценки погрешности между исходной и интерполяционной функции воспользуемся формулой:
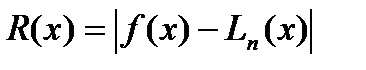
R (-2)=|-10.4147 – (-5.6636)| = 4.75115
Вывод
Мы получили значительную погрешность и для того, чтобы её снизить необходимо увеличить число узлов на заданном интервале.
ЗАДАНИЕ 2
2.1 Условие
Используя полученные на предыдущем этапе точки построить аппроксимирующие полиномы второго порядка у = a2х2 + a1x + a0 методом наименьших квадратов при всех одинаковых весовых коэффициентах и при весовом коэффициенте в третьей точке в 3 раза большем, чем в остальных (т.е. при 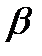 3=3). Получить среднеквадратичную погрешность аппроксимации, величину квадратичного критерия близости и расчётное значение y в третьей точке. Сравнить полученные результаты. Сделать выводы о том, устраивает ли полученное аппроксимирующее уравнение второго порядка по погрешности, сравнивая среднеквадратичную погрешность с заданной погрешностью в обоих случаях, т.е. и при всех одинаковых весовых коэффициентах и при
3=3). Получить среднеквадратичную погрешность аппроксимации, величину квадратичного критерия близости и расчётное значение y в третьей точке. Сравнить полученные результаты. Сделать выводы о том, устраивает ли полученное аппроксимирующее уравнение второго порядка по погрешности, сравнивая среднеквадратичную погрешность с заданной погрешностью в обоих случаях, т.е. и при всех одинаковых весовых коэффициентах и при 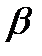 3=3. Если результат не устраивает, то наметить путь, что делать в таком случае дальше. Также проанализировать, как повлияло введение весового коэффициента
3=3. Если результат не устраивает, то наметить путь, что делать в таком случае дальше. Также проанализировать, как повлияло введение весового коэффициента 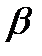 3=3 на точность аппроксимации в третьей точке (по величине абсолютной погрешности в этой точке) и на точность аппроксимации в целом, (по величине критерия близости).
3=3 на точность аппроксимации в третьей точке (по величине абсолютной погрешности в этой точке) и на точность аппроксимации в целом, (по величине критерия близости).
Примечание: Задача аппроксимации, таким образом, выполняется дважды. В обоих случаях необходимо привести выводы всех расчётных формул и алгоритм расчёта, а не просто результат по готовому пакету программ.
2.2 Решение
Зачётная книжка № Д-12091; N10 = 91/10 остаток 1
2.2.1 Исходные данные из предыдущей задачи
f(x) = x + 10sin(x+1); интервал [-10;5/4]
Таблица 3 – исходные данные
| Номер узла | Значение аргумента, x | Значение функции, f(x) |
| 0 | -10 | -14.1212 |
| 1 | -7 | -4,20585 |
| 2 | -4,5 | -0,99217 |
| 3 | -1.5 | -6,294 |
| 4 | 1,25 | 9,030732 |
2.2.2 Определение аппроксимирующей функции при помощи метода наименьших квадратов для равных весовых коэффициентов
В общем случае квадратичный критерий близости равен:
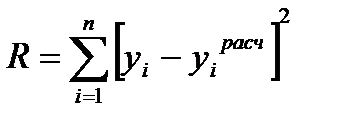 ; (1)
; (1)
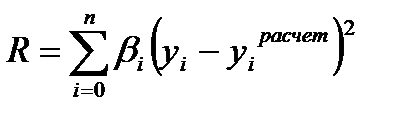 ; (2)
; (2)
где 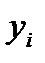 - заданные табличные значения функции;
- заданные табличные значения функции;
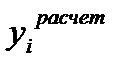 - расчетные значения по аппроксимирующей функции;
- расчетные значения по аппроксимирующей функции;
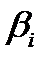 - весовые коэффициенты, учитывающие относительную важность i -й
- весовые коэффициенты, учитывающие относительную важность i -й
точки.
В качестве аппроксимирующего уравнения выбираем уравнение второго порядка с n =5:
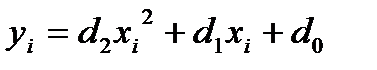 ; (3)
; (3)
В качестве критерия близости – критерий (1).
Из математического условия минимума функции R, после постановки уравнения (3) в выражение (1) принимает вид:
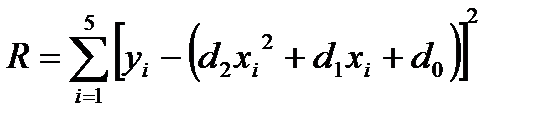 ; (4)
; (4)
R = f (d0; d1; d2) – является равенством 0, частных производных этой функции.
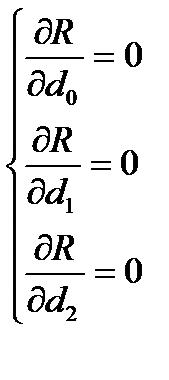 - математическое условие. (5)
- математическое условие. (5)
Из решения системы (5) находим коэффициенты d0; d1; d2 .
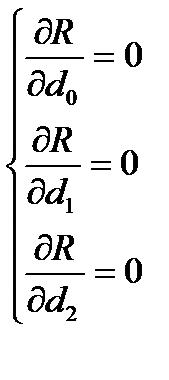 Þ
Þ 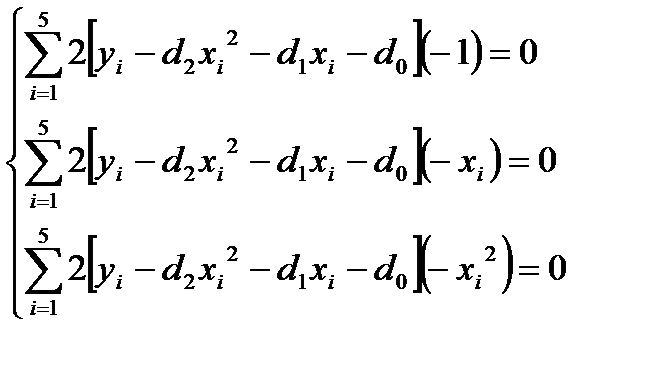
После преобразования (сокращения на два, раскрытия скобок, изменения порядка суммирования) получим:
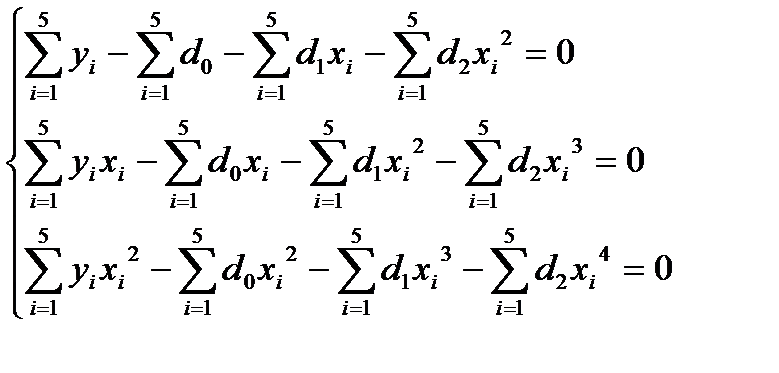 Þ
Þ 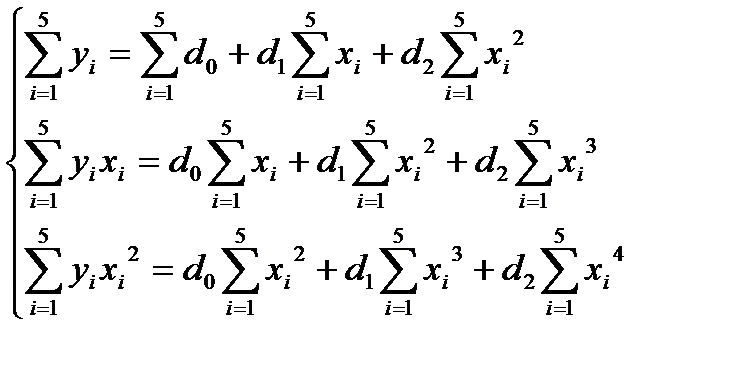 (6)
(6)
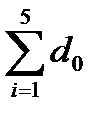 = 5 d 0;
= 5 d 0;
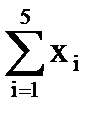 = -10 – 7 - 4,5 - 1,5 + 1,25 = -21,75
= -10 – 7 - 4,5 - 1,5 + 1,25 = -21,75
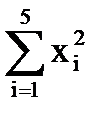 = (-10)2 + (-7)2 + (-4,5)2 + (-1,5)2 +1,252 = 173,0625
= (-10)2 + (-7)2 + (-4,5)2 + (-1,5)2 +1,252 = 173,0625
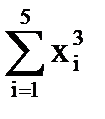 = (-10)3 + (-7)3 + (-4,5)3 + (-1,5)3 +1,253 = -1435,547
= (-10)3 + (-7)3 + (-4,5)3 + (-1,5)3 +1,253 = -1435,547
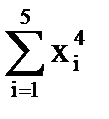 = (-10)4 + (-7)4 + (-4,5)4 + (-1,5)4 +1,254 = 12818,566
= (-10)4 + (-7)4 + (-4,5)4 + (-1,5)4 +1,254 = 12818,566
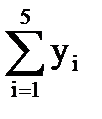 = -14,1212 - 4,20585 - 0,99217 - 6,294 + 9,030732 = -16,58
= -14,1212 - 4,20585 - 0,99217 - 6,294 + 9,030732 = -16,58
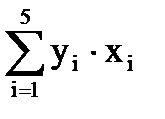 = -14,1212×(-10)+(- 4,20585)×(-7)+(- 0,99217)×(-4,5)+(- 6,294)×(-1,5) +
= -14,1212×(-10)+(- 4,20585)×(-7)+(- 0,99217)×(-4,5)+(- 6,294)×(-1,5) +
+ 9,030732×1,25 =195,84713
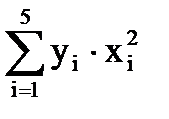 = -14,1212×(-10)2+(- 4,20585)×(-7)2+(- 0,99217)×(-4,5)2+(- 6,294)×(-1,5)2+
= -14,1212×(-10)2+(- 4,20585)×(-7)2+(- 0,99217)×(-4,5)2+(- 6,294)×(-1,5)2+
+ 9,030732×1,252 = -1638,3
С учётом полученных данных система (6) принимает вид:
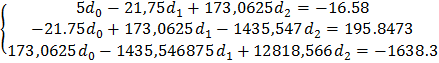 (7)
(7)
Из системы уравнений (7) находим:
d 0 = 3,589, d 1 = 1,697, d 2 = 0,0138.
Аппроксимирующий полином второго порядка при равенстве весовых коэффициентов имеет вид:
у = 0,014х2 + 1,698x + 3,59.
Составим таблицу, в которую запишем как расчётные у, так и значения f(x).
Таблица 4 – Значения f(x), y расч при равных коэффициентах.
| x | f(x) | y расч |
| -10 | -14,1212 | -11,99 |
| - 7 | -4,20585 | -7,61 |
| - 4,5 | -0,99217 | -3,7675 |
| - 1,5 | -6,294 | 1,0745 |
| 1,25 | 9,030732 | 5,734375 |
Квадратичный критерий близости:
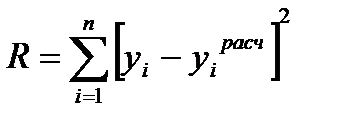 = (-14,1212+11,99)2+(-4,20585+7,61)2+(-0,99217+3,7675)2+
= (-14,1212+11,99)2+(-4,20585+7,61)2+(-0,99217+3,7675)2+
+(-6,294-1,0745)2+(9,030732-5,734375) = 88,99721
Среднеквадратичная погрешность аппроксимации:
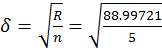 = 4.218939
= 4.218939
2.2.3 Определение аппроксимирующей функции при помощи метода наименьших квадратов при неравных весовых коэффициентах
b1= b2= b4 =b5=1; b3=3
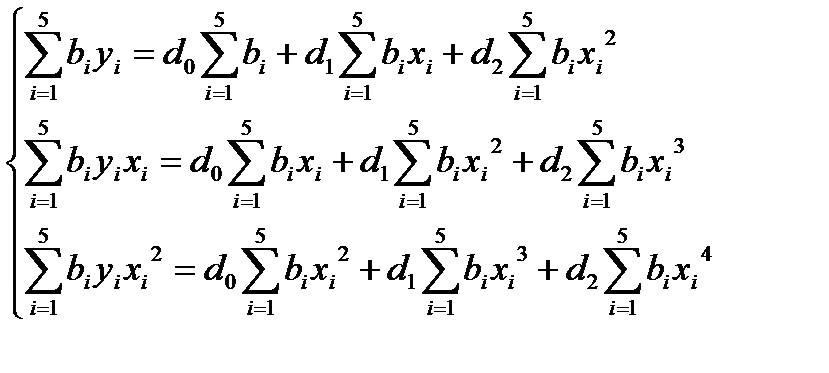 (8)
(8)
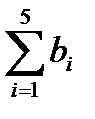 = 1 + 1 + 3 + 1 + 1 = 7
= 1 + 1 + 3 + 1 + 1 = 7
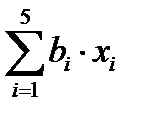 = -10 – 7 + 3×(-4,5) - 1,5 + 1,25 = -30,75
= -10 – 7 + 3×(-4,5) - 1,5 + 1,25 = -30,75
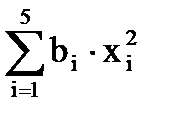 = (-10)2 + (-7)2 + 3×(-4,5)2 - (1,5)2 + 1,252 = 213,5625
= (-10)2 + (-7)2 + 3×(-4,5)2 - (1,5)2 + 1,252 = 213,5625
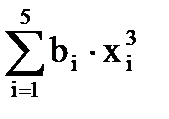 = (-10)3 + (-7)3 + 3×(-4,5)3 - (1,5)3 + 1,253= -1617,797
= (-10)3 + (-7)3 + 3×(-4,5)3 - (1,5)3 + 1,253= -1617,797
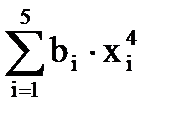 = (-10)4 + (-7)4 + 3×(-4,5)4 - (1,5)4 + 1,254 = 13638,69
= (-10)4 + (-7)4 + 3×(-4,5)4 - (1,5)4 + 1,254 = 13638,69
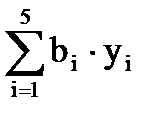 = -14,1212 - 4,20585 +3×(- 0,99217) - 6,294 + 9,030732 = -18,567
= -14,1212 - 4,20585 +3×(- 0,99217) - 6,294 + 9,030732 = -18,567
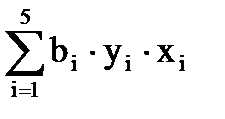 = -14,1212×(-10)+(- 4,20585)×(-7)+3×(- 0,99217)×(-4,5)+(- 6,294)×(-1,5)+
= -14,1212×(-10)+(- 4,20585)×(-7)+3×(- 0,99217)×(-4,5)+(- 6,294)×(-1,5)+
+ 9,030732×1,25 = 204,7768
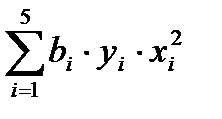 =-14,1212×(-10)2+(-4,20585)×(-7)2+3×(-0,99217)×(-4,5)2+(-6,294)×(1,5)2 + +9,030732×1,252 = -16,78,5
=-14,1212×(-10)2+(-4,20585)×(-7)2+3×(-0,99217)×(-4,5)2+(-6,294)×(1,5)2 + +9,030732×1,252 = -16,78,5
С учётом полученных данных система (8) принимает вид:
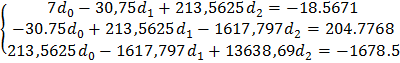 (9)
(9)
Из системы уравнений (9) находим:
d 0 = 3,97, d 1 = 1,2549, d 2 = -0,036.
Аппроксимирующий полином второго порядка при равенстве весовых коэффициентов имеет вид:
у = 0,036х2 + 1,2549x + 3,97.
Составим таблицу, в которую запишем как расчётные у, так и значения f(x).
Таблица 5 – Значения f(x), y расч при неравных коэффициентах.
| x | f(x) | y расч |
| -10 | -14,1212 | -12,179 |
| - 7 | -4,20585 | -6,593 |
| - 4,5 | -0,99217 | -2,40425 |
| - 1,5 | -6,294 | 2,01175 |
| 1,25 | 9,030732 | 5,4746875 |
Квадратичный критерий близости:
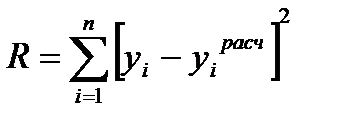 = (-14,1212+12,179)2+(-4,20585+6,593)2+(-0,99217+2,40425)2+
= (-14,1212+12,179)2+(-4,20585+6,593)2+(-0,99217+2,40425)2+
+(-6,294-2,01175)2+(9,030732-5,4746875) = 93,09975
Среднеквадратичная погрешность аппроксимации:
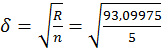 = 4.315084
= 4.315084
2.2.4 Построение графиков при помощи среды Excel 2013
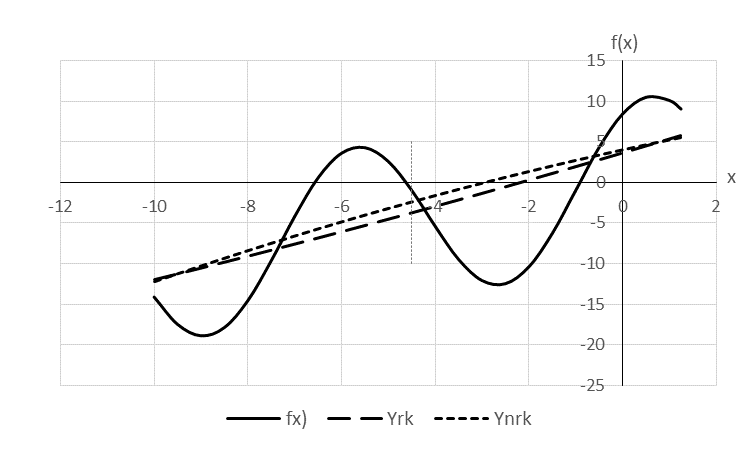
Рис.2 - Графики аппроксимирующих полиномов и исходной функции.
f(x) – исходная функция; Yrk(x) – расчетная аппроксимирующая функция с равными весовыми коэффициентами; Ynrk(x) – расчетная аппроксимирующая функция с неравными весовымикоэффициентами.
2.2.5 Расчетные значения аппроксимирующей функции третьей точке равной -4,5
Расчетные значениядля равных коэффициентов:
y расч(-4.5) = 0.14×(-4.5)2+1.698×(-4.5)+3.59 = -3.7675
Расчетные значениядля неравных коэффициентов:
y расч(-4.5) = 0.036×(-4.5)2+1.2549×(-4.5)+3.97 = -2.40425
Расчетные значениядля исходной функции:
y (-4.5) = -4.5 + 10sin(-4.5+1) = -0.99217
2.2.6 Вывод
Сравнивая расчетные значения аппроксимирующих функций в третьей точке x = -4,5 и построенных графиков функций (рисунок 2), можно сделать вывод, что аппроксимирующий полином с весовым коэффициентом 3 при точке х = -4,5 более точно описывает исходную функцию в окрестности этой точки. Однако повышение точности в одной точке вызывает увеличение среднеквадратической погрешности, а также величину квадратичного критерия близости, что связано с ухудшением аппроксимации в остальных точках.
ЗАДАНИЕ 3
3.1 Условие
Дано уравнение f(х) = 0. Отделить корни в интервале [а, b] и уточнить один из них (любой на выбор) заданным методом. Разработать блок-схему алгоритма используемого метода. Результаты представить в виде таблицы
(i - хi - f(хi)), и графиков в координатах хi - f(хi), где i – номер шага (итерации).
Отделение корней произвести аналитическим или графическим методом, если аналитический метод окажется затруднительным. Уточнение корней произвести одним методом. Метод уточнения корней выбрать по числу N6+1 из общего списка методов. Погрешность решения принять равной: 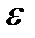 = 0.01.
= 0.01.
Решение
Зачётная книжка № Д-12091
N10 = 91/10 остаток 1; N6 = 91/6 = 15(остаток 1); N6 + 1 = 1+1 = 2
3.2.1 Исходные данные
f(x) = x + 10sin(x+1); интервал [-10;5]
Уточнение корней производим методом деления отрезка пополам.
3.2.2 Определение корней функции на интервале [-10;5] графическим методом
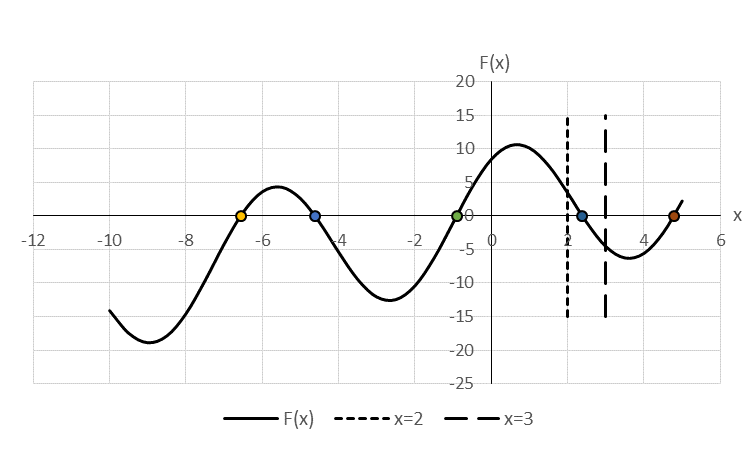
Рис.3 - Определение корней функции графическим методом.
У функции f(x) = x + 10sin(x+1) на отрезке [-10;5] имеется пять корней:
х1 » -6,56678; х2 » -62208; х3 » -0,908977; х4» 2,3821; х5 » 4,78432
3.2.3 Уточнение корней методом деления отрезка пополам
Выберем корень х 4 расположенный на интервале [2,3], который уточнимметодом деления отрезка пополам с погрешностью ε = 0,01.
Метод методом деления отрезка пополам заключается в следующем:
Вычисляем f (a), определяем половину отрезка х = (a+b)/2 и вычисляем f(х).
Проверяем следующие условия:
a) Если f(х)× f(a) < 0, то корень лежит в интервале [ a,х ].
b) Если f(х)× f(a) > 0, то корень лежит в интервале [ х,b].
c) Если b-a < ε, то х является корнем
Шаг1.
Находим середину отрезка [2; 3]:
f (а) = 3,4112
х = (2 + 3)/2 = 2,5
f(x) = -1,00783
Поскольку f (а) × f(x) < 0, то х= b = 2,5
Шаг 2.
Находим середину отрезка [2; 2,5]:
f (а) = 3,4112
х = (2 + 2,5)/2 = 2,25
f(x) = 1,168049
Поскольку f (а) × f(x) > 0, то х= а = 2,25
Шаг 3.
Находим середину отрезка [2,25; 2,5]:
f (а) = 1,168049
x = (2,25 + 2,5)/2 = 2,375
f(x) = 0,062062
Поскольку f (а)× f(x) > 0, то х = а = 2,375
Шаг 4.
Находим середину отрезка [2,375; 2,5]:
f (а) =0,062062
x = (2,375 + 2,25)/2 = 2,4375
f(x) = -0,47858
Поскольку f (а)× f(x) < 0, то х = b = 2,4375
Шаг 5.
Находим середину отрезка [2,375;2,4375]:
f (а) =0,062062
x = (2,375 + 2,4375)/2 = 2.40625
f(x) = -0.20954
Поскольку f (a)× f(x) < 0, то х = b = 2,40625
Шаг 6.
Находим середину отрезка [2,375;2,40625]:
f (а) =0,062062
x = (2,375 + 2,40625)/2 = 2.390625
f(x) = -0.07404; f (a)× f(x) < 0, то х = b = 2,390625
Шаг 7.
Находим середину отрезка [2,375;2,390625]:
f (а) =0,062062
x = (2,375 + 2,390625)/2 = 2.382813
f(x) = -0.00606; f (a)× f(x) < 0, то х = b = 2,382813
Шаг 8.
Находим середину отрезка [2,375;2,382813]:
f (а) =0,062062
x = (2,375 + 2,382813)/2 = 2.378907
f(x) = 0.02798; f (a)× f(x) > 0, то х = a = 2,378907
Шаг 9.
Находим середину отрезка [2,378907;2,382813]:
f (а) =0,02798
x = (2,378907 + 2,382813)/2 = 2.38086
f(x) = 0.010951; f (a)× f(x) > 0, то х = a = 2,38086
Шаг 10.
Находим середину отрезка [2,38086;2,382813]:
f (а) =0,02798
x = (2,378907 + 2,382813)/2 = 2,381837; f(x) = f (a)× f(x) > 0, то х = a = 2,381837
Так как b – a = 2,382813 - 2,38086 = 0,002441734 < 0.01, то х = 2,381837является корнем с погрешностью ε = 0,01.
3.2.4 Полученные результаты представим в виде таблицы (i - хi - f(хi)) и графиков в координатах хi - f(хi), где i – номер шага (итерации)
Таблица 6 – Уточнение корней методом деления отрезка пополам.
| i | xi | f(xi) |
| 1 | 2,5 | -1,00783 |
| 2 | 2,25 | 1,168049 |
| 3 | 2,375 | 0,062062 |
| 4 | 2,4375 | -0,47858 |
| 5 | 2,40625 | -0,20954 |
| 6 | 2,390625 | -0,07404 |
| 7 | 2,382813 | -0,00606 |
| 8 | 2,378907 | 0,02798 |
| 9 | 2,38086 | 0,010951 |
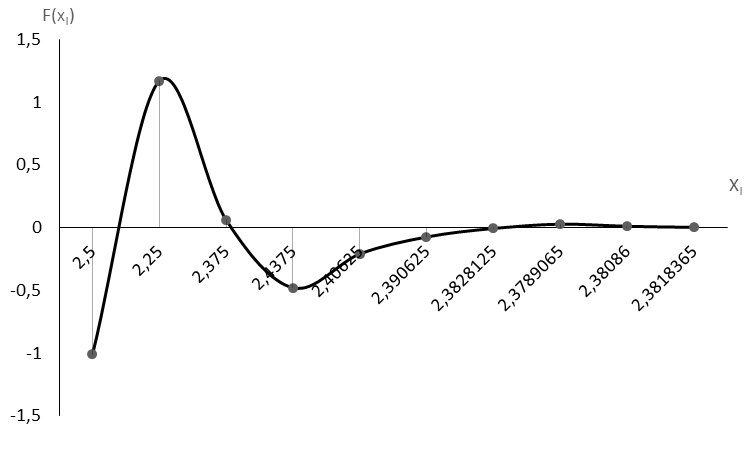
Рис.4 - График уточнение корней методом деления отрезка пополам.
3.2.5 Построение блок-схемы алгоритма уточнение корней методом деления отрезка пополам
3.2.5 Вывод
х граф.знач.» 2,3821; f (2,3821) = 0,000145994
xi = 2,381837 ; f (xi) = 0,001953. Количество шагов, i = 10
Найденные значения xi методом деления отрезка пополам с погрешность
ε = 0,01 соответсвуют значению корня функции f(x) = x + 10sin(x+1) на отрезке [2; 3].
ЗАДАНИЕ 4
4.1 Условие
По заданной функции f(х) в заданном интервале рассчитать интеграл 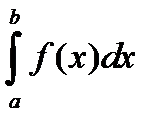 заданным методом (интервал [а, b] разбить не менее чем на шесть подынтервалов). Метод численного интегрирования выбрать по числу N4+1 из следующего общего списка методов:
заданным методом (интервал [а, b] разбить не менее чем на шесть подынтервалов). Метод численного интегрирования выбрать по числу N4+1 из следующего общего списка методов:
1. Простейшие методы
2. Метод Симпсона
3. Метод Ньютона-Котеса
4. Методы Чебышева и Гаусса
4.2 Решение
Зачётная книжка № Д-12091
N10 = 91/10 остаток 1; N4 = 91/4 = 22(остаток 3); N4+1 = 3+1 = 4
4.2.1 Исходные данные
f(x) = x + 10sin(x+1); интервал [-10;5]
Методы Чебышева и Гаусса.
4.2.2 Рассчитаем интеграл методом Чебышева
Разделим интервал [-10; 5] на 10 подынтервалов.Шаг интегрирования будет равен:
h = 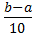
где: k примем равное 4
h = 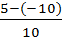 = 1.5
= 1.5
Так как шаг у нас одинаковый, то весовые коэффициенты 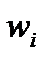 для всех подынтервалов будут одинаковыми. Высчитаем
для всех подынтервалов будут одинаковыми. Высчитаем 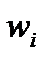 для первого подынтервала [-10;-8.5]:
для первого подынтервала [-10;-8.5]:
w1= 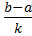 =
= 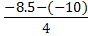 = 0.375
= 0.375
Следовательно для всех подынтервалов 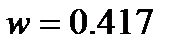 .
.
Интеграл для i – подынтервала:
I=wi× 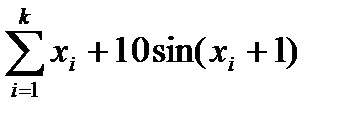
хi высчитывается по формуле: 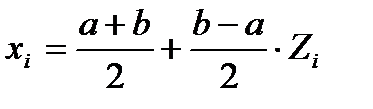 .
.
где Zi при k = 4 будут равны:
Z1= -0,794654; Z2= -0,187592; Z3= 0,187592; Z4 = 0,794654.
Найдем значения интеграла на интервале [-10;-8.5]:
х1 = (-10+(-8,5))/2+(-8,5-(-10)/2×(-0,794654) = -9,84599
х2 = -9,25 + 0,75×(-0,187592) = -9,39069
х3 = -9,25 + 0,75×0,187592 = -9,10931
х4 = -9,25 + 0,75×0,794654 = -8,65401
I1 = Zi ×(f(x1) + f(x2)+ f(x3)+ f(x4)) = 0.375×(-15.3161 -17.9846 -18.7851 - 26.4527) =
= -26.4527
Найдем значения интеграла на интервале [-8.5;-7]:
х1 = -7,75+0,75×(-0,794654) = -8,34599
х2 = -7,75 + 0,75×(-0,187592) = -7,89069
х3 = -7,75 + 0,75×0,187592 = -7,60931
х4 = -7,75 + 0,75×0,794654 = -7,15401
I2 = 0,375×(-17,0,832-13,5989-10,813-5,86587) = -17,7604
Найдем значения интеграла на интервале [-7;-5,5]:
х1 = -6,25+0,75×(-0,794654) = -6,84599
х2 = -6,25 + 0,75×(-0,187592) = -6,3906
х3 = -6,25 + 0,75×0,187592 = -6,10931
х4 = -6,25 + 0,75×0,794654 = -5,65401
I3 = 0,375×(-2,61199 + 1,39568 + 3,113259 + 4,32895) = 2,334712
Найдем значения интеграла на интервале [-5,5;-4]:
х1 = -4,75+0,75×(-0,794654) = -5,34599
х2 = -4,75 + 0,75×(-0,187592) = -4,89069
х3 = -4,75 + 0,75×0,187592 = -4,60931
х4 = -4,75 + 0,75×0,794654 = -4,15401
I4 = 0,375×(3,990246 +1,919116 – 0,10083 - 4,02982) = 0,667018
Найдем значения интеграла на интервале [-4;-2,5]:
х1 = -3,25+0,75×(-0,794654) = -3,84599
х2 = -3,25 + 0,75×(-0,187592) = -3,39069
х3 = -3,25 + 0,75×0,187592 = -3,10931
х4 = -3,25 + 0,75×0,794654 = -2,65401
I5 = 0,375×(-6,75915 -10,2137 – 11,694 - -12,6194) = -15,4823
Найдем значения интеграла на интервале [-2,5;-1]:
х1 = -1,75+0,75×(-0,794654) = -2,34599
х2 = -1,75 + 0,75×(-0,187592) = -1,89069
х3 = -1,75 + 0,75×0,187592 = -1,60931
х4 = -1,75 + 0,75×0,794654 = -1,15401
I6 = 0,375×(-12,0944 – 9,66578 – 7,3323 – 2,68806) = -11,9177
Найдем значения интеграла на интервале [-1; 0,5]:
х1 = -0,25+0,75×(-0,794654) = -0,84599
х2 = -0,25 + 0,75×(-0,187592) = -0,39069
х3 = -0,25 + 0,75×0,187592 = -0,10931
х4 = -0,25 + 0,75×0,794654 = 0,345988
I7 = 0,375×(0,688023 + 5,332291 + 7,665767 + 10,09435) = 8,917664
Найдем значения интеграла на интервале [0,5; 2,5]:
х1 = 1,25+0,75×(-0,794654) = 0,65401
х2 = 1,25 + 0,75×(-0,187592) = 1,109306
х3 = 1,25 + 0,75×0,187592 = 1,390693
х4 = 1,25 + 0,75×0,794654 = 1,845988
I8 = 0,375×(10,61941 + 9,694046 + 8,213664 + 12,48236) = 12,48236
Найдем значения интеграла на интервале [2,5; 3,5]:
х1 = 2,75+0,75×(-0,794654) = 2,15401
х2 = 2,75 + 0,75×(-0,187592) = 2,609306
х3 = 2,75 + 0,75×0,187592 = 2,890693
х4 = 2,75 + 0,75×0,794654 = 3,345988
I9 = 0,375×(2,029844 – 1,89916 – 3,91911 – 5,99024) = -3,667
Найдем значения интеграла на интервале [0,5; 2,5]:
х1 = 4,25+0,75×(-0,794654) = 3,65401
х2 = 4,25 + 0,75×(-0,187592) = 4,109306
х3 = 4,25 + 0,75×0,187592 = 4,390693
х4 = 4,25 + 0,75×0,794654 = 4,845988
I10 = 0,375×(-6,32895 – 5,11327 – 3,39569 + 0,61962) = -5,33473
Общий интеграл для функции f(x) = x + 10sin(x+1) на отрезке [-10; 5] будет равен сумме всех интегралов для подынтервалов:
Iобщ=  = I1 + I2 + I3 + I4 + I5 + I6 + I7 + I8 + I9 + I10 = -26,4527 –17,7604 +2,334712 + +0,667018- 15,4823 – 11,9177 + 8,917664 + 12,48236 – 3,667 – 5,33473 = -56,2131
= I1 + I2 + I3 + I4 + I5 + I6 + I7 + I8 + I9 + I10 = -26,4527 –17,7604 +2,334712 + +0,667018- 15,4823 – 11,9177 + 8,917664 + 12,48236 – 3,667 – 5,33473 = -56,2131
4.2.2 Рассчитаем интеграл методом Гаусса
В методе Гаусса интеграл для i – подынтервала будет вычисляться по
формуле:
I= 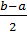 ×
× 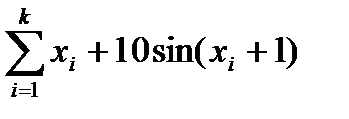
хi вычисляется также как в методе Чебышева:
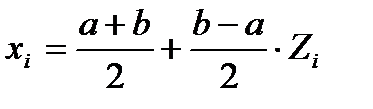 .
.
Но wi будет зависеть от значения k и Zi будет равно вметоде Чебышева
Значения wi и Zi при k =4:
-Z1 = Z4 = 0,861136; -Z2 = Z3=0,33998;
w1 = w4 = 0,3447855; w2 = w3 = 0,652145.
Найдем значения интеграла на интервале [-10;-8.5]:
х1 = -9,25+0,75×(-0,861136) = -9,89585
х2 = -9,25 + 0,75×(-0,339981) = -9,50499
х3 = -9,25 + 0,75×0,339981 = -8,99501
х4 = -9,25 + 0,75×0,861136 = -8,60415
I1 = 0,75×(0,347855×(-14,9419) + 0,625145×(–17,4597) + 0,625145×(–18,8957) +
+ 0,347855×(-18,2937)) = -26,4527
Найдем значения интеграла на интервале [-8.5;-7]:
х1 = -7,75+0,75×(-0,861136) = -8,39585
х2 = -7,75 + 0,75×(-0,339981) = -8,00499
х3 = -7,75 + 0,75×0,339981 = -7,49501
х4 = -7,75 + 0,75×0,861136 = -7,10415
I2 = 0,75×(0,347855×(-17,3647) + 0,625145×(–14,6124) + 0,625145×(–9,5975) +
+ 0,347855×(-5,32332)) = -17,7603
Найдем значения интеграла на интервале [-7;-5,5]:
х1 = -6,25+0,75×(-0,861136) = -6,89585
х2 = -6,25 + 0,75×(-0,339981) = -6,50499
х3 = -6,25 + 0,75×0,339981 = -5,99501
х4 = -6,25 + 0,75×0,861136 = -5,60415
I3 = 0,75×(0,347855×(-3,11865) + 0,625145×0,514997 + 0,625145×3,608252 +
+ 0,347855×4,337329) = 2,334661
Найдем значения интеграла на интервале [-5.5;-4]:
х1 = -4,75+0,75×(-0,861136) = -5,39585
х2 = -4,75 + 0,75×(-0,339981) = -5,00499
х3 = -4,75 + 0,75×0,339981 = -4,49501
х4 = -4,75 + 0,75×0,861136 = -4,10415
I4 = 0,75×(0,347855×4,107339 + 0,625145×2,595534 + 0,625145×(-1,03391) +
+ 0,347855×(-4,47851)) = 0,666967
Найдем значения интеграла на интервале [-4;-2,5]:
х1 = -3,25+0,75×(-0,861136) = -3,89585
х2 = -3,25 + 0,75×(-0,339981) = -3,50499
х3 = -3,25 + 0,75×0,339981 = -2,99501
х4 = -3,25 + 0,75×0,861136 = -2,60415
I5 = 0,75×(0,347855×(-6,3286) + 0,625145×(-9,44969) + 0,625145×(-12,1086) +
+ 0,347855×(-12,5986)) = -15,4823
Найдем значения интеграла на интервале [-2,5;-1]:
х1 = -1,75+0,75×(-0,861136) = -2,39585
х2 = -1,75 + 0,75×(-0,339981) = -2,00499
х3 = -1,75 + 0,75×0,339981 = -1,49501
х4 = -1,75 + 0,75×0,861136 = -1,10415
I6 = 0,75×(0,347855×(-12,2432) + 0,625145×(-10,4465) + 0,625145×(-6,24546) +
+ 0,347855×(-2,14375)) = -11,9176
Найдем значения интеграла на интервале [-1; 0,5]:
х1 = -0,25+0,75×(-0,861136) = -0,89589
х2 = -0,25 + 0,75×(-0,339981) = -0,50499
х3 = -0,25 + 0,75×0,339981 = 0,004986
х4 = -0,25 + 0,75×0,861136 = 0,39852
I7 = 0,75×(0,347855×0,143746 + 0,625145×4,245456 + 0,625145×8,446529 +
+ 0,347855×10,24321) = 8,917628
Найдем значения интеграла на интервале [0,5; 2]:
х1 = 1,25+0,75×(-0,861136) = 0,604148
х2 = 1,25 + 0,75×(-0,339981) = 0,995014
х3 = 1,25 + 0,75×0,339981 = 1,504986
х4 = 1,25 + 0,75×0,861136 = 1,89852
I8 = 0,75×(0,347855×10,59859 + 0,625145×10,10862 + 0,625145×7,44969 +
+ 0,347855×4,3286) = 12,4823
Найдем значения интеграла на интервале [2; 3,5]:
х1 = 2,75+0,75×(-0,861136) = 2,104148
х2 = 2,75 + 0,75×(-0,339981) = 2,495014
х3 = 2,75 + 0,75×0,339981 = 3,004986
х4 = 2,75 + 0,75×0,861136 = 3,39852
I9 = 0,75×(0,347855×2,478507 + 0,625145×(-0,96609) + 0,625145×(-4,59553) +
+ 0,347855×(-6,10734)) = -3,66697
Найдем значения интеграла на интервале [3,5; 5]:
х1 = 4,25+0,75×(-0,861136) = 3,604148
х2 = 4,25 + 0,75×(-0,339981) = 3,995014
х3 = 4,25 + 0,75×0,339981 = 4,504986
х4 = 4,25 + 0,75×0,861136 = 4,89852
I10 = 0,75×(0,347855×(-6,33733) + 0,625145×(-5,60825) + 0,625145×(-2,515) +
+ 0,347855×1,118646) = -5,33466
Общий интеграл для функции будет равен сумме всех интегралов для подынтервалов:
Iобщ=  = I1 + I2 + I3 + I4 + I5 + I6 + I7 + I8 + I9 + I10 = -26,4527 –17,7603 +2,334661 + + 0,666967 - 15,4823 – 11,9176 + 8,917628 + 12,4823 – 3,66697 – 5,33466 =
= I1 + I2 + I3 + I4 + I5 + I6 + I7 + I8 + I9 + I10 = -26,4527 –17,7603 +2,334661 + + 0,666967 - 15,4823 – 11,9176 + 8,917628 + 12,4823 – 3,66697 – 5,33466 =
= -56,2130
Вывод
Общий интеграл для функции f(x) = x + 10sin(x+1) на отрезке [-10; 5] равен:
По методу Чебышева:
-56,2131
По методу Гаусса:
-56,2130
Мы видим, что интегралы для функции высчитанные по методам Чебышева и Гаусса отличаются на одну десятитысячную. Это объясняется тем, что в методе Гаусса весовые коэффициенты различные, поэтому он более точный.
ЗАДАНИЕ 5
5.1 Условие
Задана система нелинейных уравнений:
f1(x1,x2) = 0,
f2(x1,x2) = 0.
Уравнения системы выбираются изтаблицы № 2 в зависимости от числа N10. Требуется решить эту систему заданным в соответствии с номером варианта методом. Метод выбрать по числу N2+1 из следующего списка:
2. Метод итераций.
5.2 Решение
Зачётная книжка № Д-12091
N10 = 91/10 остаток 1; N2 = 91/2 = 45(остаток 1); N4+1 = 1+1 = 2
5.2.1 Исходные данные
| N10 | f1(x1,x2) | f2(x1,x2) |
| 1 | x 1-cos x 2 = 3 | sin x 1 + 2 x 2 = 2 |
Метод итераций.
5.2.2 Решение системы уравнений методом итераций
Систему уравнений:
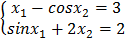
Приведём к следующему виду:
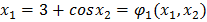
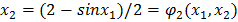 В качестве начальных условий принимаем х1 = 1 и х2 = 0,25.
В качестве начальных условий принимаем х1 = 1 и х2 = 0,25.
Проверим выполнения условий сходимости:
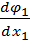 = 0,
= 0, 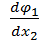 = -sin x 2,
= -sin x 2, 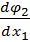 = -0,5cos x 2,
= -0,5cos x 2, 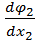 = 0,
= 0, 
Условия сходимости будут выполнятся всегда:
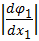 +
+  = -0,5cos x 2 < 0
= -0,5cos x 2 < 0
 +
+ 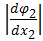 = -sin x 2 < 0
= -sin x 2 < 0
Далее будем подставлять значения х в функции, постепенно приближаясь к истинным значениям. Зададимся погрешностью ε = 0,01.
| i | x 1 | x 2 |
| cos x2 + 3 | (2 – sin x 1)/2 | |
| 1 | cos(0,25)+ 3 = 3,968912 | (2-sin(3,968912))/2=1,36806 |
| 2 | cos(1,36806)+ 3 = 3,20135 | (2-sin(3,20135))/2=1,029861 |
| 3 | cos(1,029861)+ 3 =3,514938 | (2-sin(3,514938))/2=1,182366 |
| 4 | cos(1,182366)+ 3 =3,378736 | (2-sin(3,378736))/2=1,117463 |
| 5 | cos(1,117463)+ 3 =3,437964 | (2-sin(3,437964))/2=1,146026 |
| 6 | сos(1,146026)+ 3 =3,412112 | (2-sin(3,412112))/2=1,133616 |
х 16 - х 15 = 3,412112 - 3,437964 = -0,02585 < 0,01
х 26 – х 25 = 1,133616 - 1,146026 = -0,01241 < 0,01
5.2.3 Вывод
Значения х 16 и х 26 удовлетворяют условиям: | х 1,i - х 1,i+1| < e, | х 2,i – х 2,i+1| < e, следовательно корнями уравнения системы:
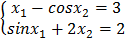
будут являться:
х 1 = 3,412112 и х 2 = 1,133616; i = 6
Сделаем проверку:
3,412112 – cos(1,133616) = 2.988725»3
sin(1,133616) +2×3,412112 = 2
Вычисления произведены верно.
ЗАДАНИЕ 7
7.1 Условие
Решить дифференциальное уравнение у' = f (х) + ху при заданных начальных условиях хо = а, у (хо)= у (а) = 0 в заданных пределах [a, b] с шагом не менее (b - а)/ 10двумя методами:
1. Методами Эйлера
2. Методом Рунге-Кутта
Итогом решения задачи должно быть построение графика полученной функции у = f (х) (минимум по 5-и точкам).
7.2 Решение
Зачётная книжка № Д-12091; N10 = 91/10 остаток 1.
7.2.1 Исходные данные
f(x) = x + 10sin(x +1); интервал [-10;5]
хо = -10, у (хо)= у (а) = 0; h = (5 – (-10))/ 10 = 1,5
7.2.2 Решение дифференциального уравнения методами Эйлера
у ' = x + 10sin(x +1) + ху;
7.2.2.1 Метод Эйлера
В общем случае метод Эйлера заключается в нахождении yi +1 по формуле:
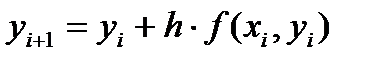
Для данного задания можно переписать как:
yi+ 1 = yi + 1.5 ×(х +10sin(x + 1) + xi yi)
Первый и последующие шаги:
y 1 = 0 + 1.5 ×(-10 +10sin(- 10 + 1) + (-10) × 0) = -21,182
y 2 = -21,182 + 1.5 ×(-8,5 +10sin(- 8,5 + 1) + (-8,5) × (-21,182) = 222,066
y 3 = 222,066 + 1.5 ×(-7 +10sin(- 7 + 1) + (-7) × 222,066 = -2115,935
y 4 = -2115,935 + 1.5 ×(-5,5 +10sin(- 5,5 + 1) + (-5,5) × (-2115,935) = 15346.939
y 5 = 15346,939 + 1.5 ×(-4 +10sin(- 4 + 1) + (-4) ×15346,939 = -76742,813
y 6 = -76742,813+ 1.5 ×(-2,5 +10sin(- 2,5 + 1) + (-2,5) × (-76742,813) = 211024,023
y 7 = 211024,023+1.5 ×(-1 +10sin(- 1 + 1) + (-1) × 211024,023 = -105513,512
y 8 = -105513,512+1.5 ×(0,5 +10sin(0,5 + 1) + 0,5 ×(-105513,512) = -184632,933
y 9 = -184632,933 +1.5 ×(2 +10sin(2 + 1) + 2 ×(-184632,933) = -738526,615
y 10 = -738526,615+1.5 ×(3,5 +10sin(3,5 + 1) + 3,5×(-738526,615) = -4615800,756
7.2.2.2 Модифицированный метод Эйлера
В общем случае модифицированный метод Эйлера заключается в нахождении yi +1 по формуле:
yi +1 = yi + 0.5 h × [ f (x i, y i)+ f (x i+1, y i+1)]
где: yi +1 – значение найденное по методу Эйлера.
xi +1 = x + h
Первое и последующие шаги:
y 1 = y 0 + 0.5 h × [ f (x 0, y 0)+ f (x 1, y 1)] = 0 + 0,75×[(-10 +10sin(- 10 + 1) + (-10)×0) +
+(-8,5+10sin(-8,5+1)+(-8,5)×(-21,182))] = 111,033
y 2= y 1+0.5 h ×[ f (x 1, y 1)+ f (x 2, y 2)]=111,033+0,75×[(-8,5+10sin(- 8,5 + 1)+(-8,5)×111,033)+
+ (-7+10sin(-7+1)+(-7)×222,066)] = -1179,212
y 3 = -1179,212 + 0,75×[(-7+10sin(- 7 + 1) + (-7)×(-1179,212) + (-5,5+10sin(-5,5+1) +
+ (-5,5)×(-2115,935))] = 16289,935
y 4 = 16289,935+0,75×[(-5,5 +10sin(- 5,5 + 1)+(-5,5)×16289,935) + (-4+10sin(-4+1) + + (-4)× 15346,939] = -96947,716
y 5=-96947,716+0,75×[(-4 +10sin(- 4 + 1) + (-4)×(-96947,716))+(-2,5+10sin(-2,5+1) +
+ (-2,5)×(-76742,813))] = 337774,793
y 6 = 337774,793+0,75×[(-2,5+10sin(- 2,5 + 1)+(-2,5)×337774,793)+(-1+10sin(-1+1)+
+ (-1)× 211024,023)] = -453831,067
y 7= -453831,067+0,75×[(-1+10sin(- 1 + 1)+(-1)×(-453831,067)) +(0,5+10sin(0,5+1)+ +0,5×(-105513,512))] = -153018,227
y 8 = -153018,227+0,75×[(0,5+10sin(0,5 + 1) +0,5×(-153018,227)) + (2+10sin(2+1) + + 0,5×(-184632,933))] = -487339,047
y 9 = -487339,047 +0,75×[(2+10sin(2 + 1) + 2×(- 487339,047)) + (3,5+10sin(3,5+1) + + 0,5×(-738526,615))] = -3156982,131
y 10=-3156982,131+0,75×[(3,5+10sin(3,5 + 1)+3,5×(- 3156982,131))+(5+10sin(5+1)+ + 5×(-4615800,756))] = -28753316,109
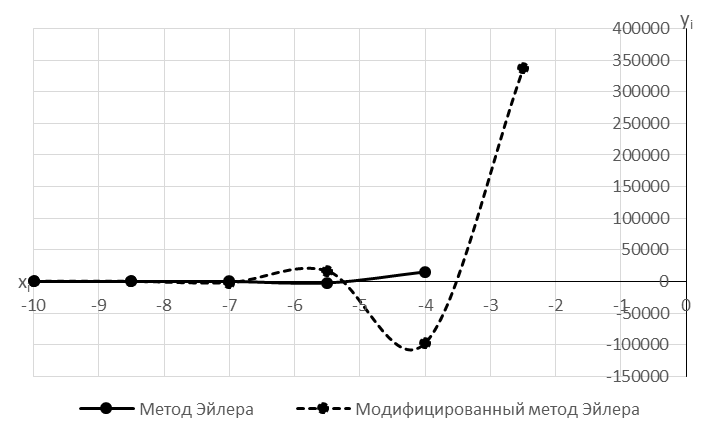
Рис. 5 – Графики функций построенные методами Эйлера.
7.2.3 Решение дифференциального уравнения методом Рунге-Кутта
Вычислительный алгоритм записывается следующим образом:
yi +1 = yi + 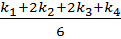
где: k1 = h× f (xi, yi);
k2 = h× f (xi +  , yi +
, yi + 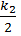 );
);
k3 = h× f (xi +  , yi +
, yi + 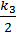 );
);
k4 = h× f (xi + h, yi + k3).
На первом шаге получим:
k1 = 1,5 ×(-10 + 10sin(-10 + 1) + (-10)×0) = -21,182
k2 = 1,5 ×(-10+1,5/2 + 10sin(-10+1,5/2 + 1) + (-10+1,5/2)×(0 - 21,182/2))= 119,235
k3 = 1,5 ×(-10+1,5/2 +10sin(-10+1,5/2+1) + (-10+1,5/2)×(0 + 119,235/2))=-854,904
k4 = 1,5 ×(-10 + 1,5 + 10sin(-10 + 1,5 + 1) + (-10 + 1,5)×(0 – 854,904))= 10873,200
y 1 =0+(-21,182+2×119,235+2×(-854,904)+10873,2)/6 = 1563,447
На втором шаге:
k1 = 1,5 ×(-8,5 + 10sin(-8,5+ 1) + (-8,5)×1563,447) = -19960,765
k2 = 1,5×(-8,5+0,75+10sin(-8,5+0,75+1)+(-8,5+0,75)×(1563,447–19960,765/2)) =
= 97828,505
k3 = 1,5 ×(-8,5+0,75+10sin(-8,5+0,75+1) + (-8,5+0,75)×(1563,447+97828,505/2)) =
= -586821,627
k4 = 1,5 ×(-7 + 10sin(-7 + 1) + (-7)×(1563,447 – 586821,627)) = 6145204,586
y 2 = 1563,447+(-19960,765+2×97828,505 +2× (-586821,627) + 6145204,586)/6 =
=859439,709
Третий шаг:
k1 = 1,5 ×(-7 + 10sin(-7+ 1) + (-7)×859439,709) = -9024123,257
k2 = 1,5×(-7+0,75 +10sin(-7+0,75+1) + (-7+0,75)×(859439,709–9024123,257/2)) =
= 34243334,0
k3 = 1,5 ×(-7+0,75+10sin(-7+0,75+1) + (-7+0,75)×(859439,709+34243334/2)) =
= -168572871,889
k4 = 1,5×(-5,5+10sin(-5,5+1)+(-5,5)×(859439,71–168572871,89))=1383635821,897
y 3 = 859439,71+(-9024123,26+2×34243334-2×168572871,89+1383635821,89)/6= = 185184876,853
Четвёртый шаг:
k1 = 1,5 ×(-5,5 + 10sin(-5,5+ 1) + (-5,5)× 185184876,853) = -1527775227,623
k2= 1,5×(-4,75+10sin(-4,75+1)-4,75×(185184876,85-1527775227,6/2))=4123257002
k3= 1,5×(-4,75+10sin(-4,75+1)-4,75×(185184876,8+4123257002/2))=-16008545316
k4 = 1,5×(-4+10sin(-4+1)-4×(185184876,853-16008545316))=94940162631,2
y 4 = 185184876,853 + (-1527775227,623 + 2×4123257002 - 2×160085453162 +
+ 1383635821,897)/6 = 11792153339,299
Пятый шаг:
k1 = 1,5 ×(-4 + 10sin(-4+ 1) - 4×11792153339,299) = -70752920043,623
k2 = 1,5×(-3,25 + 10sin(-3,25+1) - 3,25×(11792153339,299 - 70752920043/2)) =
= 114973495061,406
k3 = 1,5×(-3,25+10sin(-3,25+1) - 3,25×(11792153339,299 +114973495061,4/2)) =
= -337734641757,807
k4 = 1,5×(-2,5 + 10sin(-2,5 + 1) - 2,5×(11792153339,299 - 337734641757,807)) =
= 1222284331550,69
Y 5 =11792153339,299+(-70752920043,6+2×114973495061,4-2×337734641757,8+
+ 1222284331550,69)/6 = 129460339691,629
Шестой шаг:
k1 = 1,5 ×(-2,5 + 10sin(-2,5+ 1) – 2,5×129460339691,629) = -485476273862,321
k2 = 1,5×(-1,75 + 10sin(-1,75+1) - 1,75×(129460339691,629-485476273862,32 /2))=
= 297354217740,92
k3 = 1,5×(-1,75+10sin(-1,75+1) - 1,75×(129460339691,629+297354217740,92/2)) =
= -730110802488,333
k4= 1,5×(-1+10sin(-1+1)-1×(129460339691,62-730110802488,3))=900975694193,5
y 6 =129460339691,6+(-485476273862,32+2×297354217740,9-2×730110802488,3+
+900975694193,5)/6 = 54458048164,364
Седьмой шаг:
k1 = 1,5 ×(-1 + 10sin(-1+ 1) – 1×54458048164,364) = -8168707722248,046
k2 = 1,5×(-0,25 + 10sin(-0,25+1) - 0,25×(54458048164,364-8168707722248,04/2)) =
= -5105442005,278
k3 = 1,5×(-0,25+10sin(-0,25+1) - 0,25×(54458048164,364-5105442005,278/2)) =
= -19464497675,797
k4 = 1,5×(0,5 + 10sin(0,5+1) + 0,5×(54458048164,364 - 19464497675,797)) =
= 26245162882,137
y 7 =54458048164,364+(-8168707722248,046-2×5105442005,278-2×19464497675,7
+26245162882,137)/6 = 37027750043,021
Восьмой шаг:
k1 = 1,5 ×(0,5 + 10sin(0,5 + 1) + 0,5×37027750043,021)) = 27770812547,987
k2 = 1,5×(1,25+10sin(1,25+1)+1,25×(37027750043,01+27770812547,98/2)) =
= 95462168107,939
k3 = 1,5×(1,25+10sin(1,25+1) + 1,25×(37027750043,021+95462168107,939/2)) =
= 158922813945,403
k4 = 1,5×(2 + 10sin(2 + 1) + 2×(37027750043,021 + 158922813945,403))=
= 587851691970,387
y 8=37027750043,021+(27770812547,98+2×95462168107,9+2×158922813945,4+ +587851691970,387)/6 = 224426494813,862
Девятый шаг:
k1 = 1,5 ×(2 + 10sin(2 + 1) + 2×224426494813,862) = 673279484446,703
k2 = 1,5×(2,75+10sin(2,75+1)+2,75×(224426494813,862+673279484446,703/2)) =
= 231498227774,060
k3 = 1,5×(2,75+10sin(2,75+1) + 2,75×(224426494813,862+231498227774,060/2)) =
= 5699205635886,730
k4 = 1,5×(3,5 + 10sin(3,5 + 1) + 3,5×(224426494813,862+ 5699205635886,730))=
= 31099068686168,7
y 9=224426494813,86+(673279484446,7+2×231498227774+2×5699205635886,7+
+31099068686168,7)/6 = 8191019144470,020
Десятый шаг:
k1= 1,5×(3,5+10sin(3,5+1)+3,5×8191019144470,02)=43002850508458,200
k2 =1,5×(4,25+10sin(4,25+1)+4,25×(8191019144470,02+43002850508458,20/2))= =189289333041700
k3 = 1,5×(4,25+10sin(4,25+1) + 4,25×(8191019144470,02+189289333041700/2)) =
=655577496116410
k4 = 1,5×(5+10sin(5+1) + 5×(8191019144470,02+655577496116410/2)) =
=4978263864456600
y10 =8191019144470,02+(43002850508458,2+2×189289333041700+
+2×655577496116410+4978263864456600)/6=1126691081358020
Значения функции, полученные методом Эйлера, модифицированным методом Эйлера и методом Рунге-Кутта занесём в таблицу и построим графики функции.
Таблица 7 – Значения функции.
| шаг | xi | yi по Эйлеру | yi по модиф. Эйлеру | yi по Рунге-Кутта |
| 0 | -10 | 0 | 0 | 0 |
| 1 | -8,5 | -21,182 | 111,033 | 1563,447 |
| 2 | -7 | 222,086 | -1779,212 | 859439,709 |
| 3 | -5,5 | -2115,935 | 16289,935 | 185184876,853 |
| 4 | -4 | 15346,939 | -96947,716 | 11792153339,299 |
| 5 | -2,5 | 76742,813 | 337774,793 | 129460339691,629 |
| 6 | -1 | 211024,023 | -453831,067 | 54458048164,364 |
| 7 | 0,5 | -105513,512 | -153018,227 | 37027750043,021 |
| 8 | 2 | -184632,933 | -487339,047 | 224426494813,862 |
| 9 | 3,5 | -738526,615 | -3156982,131 | 8191019144470,02 |
| 10 | 5 | -4615800,756 | -28753316,109 | 1126691081358020 |
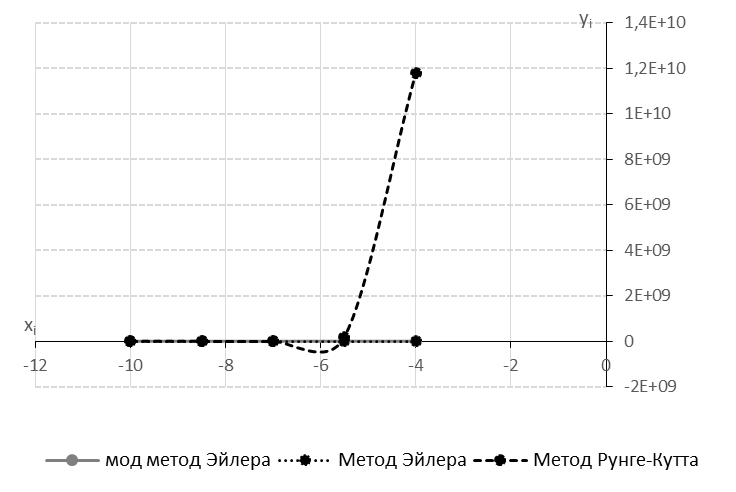
Рис.6. Графики функций по 5-ти точкам
7.2.4 Вывод
Значения функции, полученные методом Эйлера, модифицированным методом Эйлера и методом Рунге-Кутта сильно различаются. Это связано с тем, что метод Эйлера является методом решения дифференциальных уравнений первого порядка и в практических расчётах он даёт значительную погрешность. Для повышения точности используют модифицированный метод Эйлера второго порядка.
Метод Рунге-Кутта является методом четвёртого порядка, следовательно, он более точен, чем методы Эйлера.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Васильков Ю. В., Василькова Н. Н.
Компьютерные технологии вычислений в математическом моделировании: Учеб. Пособие. – М.: Финансы и статистика, 2002. – 256 с.: ил. ISBN 5-279-02098-2.
 2020-04-07
2020-04-07 2155
2155







