Пример 1. Пусть задан граф G = (X, U). Найти с помощью алгоритма Форда кратчайшие пути в заданном графе G от фиксированной вершины до всех остальных.
Решение: Рассмотрим матрицу смежности графа G:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 1 | 0 | 10 | M | M | M | M | 3 | 6 | 12 | . |
| 2 | 10 | 0 | 18 | M | M | M | 2 | M | 13 | |
| 3 | M | 18 | 0 | 25 | M | 20 | M | M | 7 | |
| R=4 | M | M | 25 | 0 | 5 | 16 | 4 | M | M | |
| 5 | M | M | M | 5 | 0 | 10 | M | 23 | M | |
| 6 | M | M | 20 | 16 | 10 | 0 | 17 | 15 | 9 | |
| 7 | 3 | 2 | M | 4 | M | 17 | 0 | M | 24 | |
| 8 | 6 | M | M | M | 23 | 15 | M | 0 | 5 | |
| 9 | 12 | 13 | 7 | M | M | 9 | 24 | 5 | 0 |
1.1. В качестве фиксированной вершины выбираем вершину x 1. Тогда ее вес V(1) = 0, а веса всех остальных вершин: V(2) = V(3) = … = V(9) = ¥ = M.
1.2. Просматриваем первую строку матрицы смежности и выбираем поочередно все вершины, не помеченные литерой M. В результате мы сформировали следующий список вершин: x 2, x 7, x 8, x 9.
1.3. Для каждой из вершин, входящих в полученный список, проверяем истинность неравенства (1.8):
V(2) = ¥ > 0 + 10 = 10; V(7) = ¥ > 0 + 3 = 3; V(8) = ¥ > 0 + 6 = 6;
V(9) = ¥ > 0 + 12 = 12.
Значения весов для вершин x 3, x 4, x 5, x 6 не изменяются.
Теперь произведем пересчет индексов для вершин смежных с x 1, с учетом пути через другие смежные вершины.
1.4. Производим пересчет весов для сформированного списка вершин:
для вершины x 2:
- V(2) > V(7) + r27 ® 10 > 3 + 2 ─ неравенство истинно, следовательно, вес вершины изменяется: V(2)1 = 5,
- V(2) > V(9) + r29 ® 10 > 1 + 13 ─ неравенство ложно, следовательно, вес вершины не изменяется;
для вершины x 7:
- V(7) > V(2) + r27 ® 3 > 10 + 2 ─ неравенство ложно, следовательно, вес вершины не изменяется;
- V(7) > V(9) + r79 ® 3 > 12 + 24 ─ неравенство ложно, следовательно, вес вершины не изменяется.
для вершины x 8:
- V(8) > V(9) + r89 ® 6 > 12 + 5 ─ неравенство ложно, следовательно, вес вершины не изменяется;
для вершины x 9:
- V(9) > V(2) + r29 ® 12 > 10 + 13 ─ неравенство ложно, следовательно, вес вершины не изменяется,
- V(9) > V(7) + r79 ® 12 > 3 + 24 ─ неравенство ложно, следовательно, вес вершины не изменяется,
- V(9) > V(8) + r89 ® 12 > 6 + 5 ─ неравенство истинно, следовательно, вес вершины изменяется: V(9)1 = 11.
1.5. Проверка условия: все ли вершины помечены.
Произведем пересчет индексов для вершин, несмежных с фиксированной вершиной x 1.
2.1. Вычислим значение веса вершины x 3, его можно найти через x 2, x 4, x 6 или x 9. Однако значения весов вершин x 4 и x 6 нам пока не известны, поэтому производим расчет через вершины x 2 и x 9:
- V(3) > V(2) + r23 ® ¥ > 5 + 18 - неравенство истинно, следовательно, вес вершины изменяется: V(3)1 = 23,
- V(3) > V(9) + r39 ® 23 > 11 + 7 ─ неравенство истинно, следовательно, вес вершины изменяется: V(3)2 = 18.
2.2. Вычислим значение веса вершины x 4, его можно найти через x 3, x 5, x 6 или x 7. Однако значения весов вершин x 5 и x 6 нам пока не известны, поэтому производим расчет через вершины x 3 и x 7:
- V(4) > V(3) + r34 ® ¥ > 18 + 25 ─ неравенство истинно, следовательно, вес вершины изменяется: V(4)1 = 43,
- V(4) > V(7) + r47 ® 43 > 3 + 4 ─ неравенство истинно, следовательно, вес вершины изменяется: V(4)2 = 7.
2.3. Вычислим значение веса вершины x 5, его можно найти через x 4, x 6 или x 8. Однако значение веса вершины x 6 нам пока не известно, поэтому производим расчет через вершины x 4 и x 8:
- V(5) > V(4) + r45 ® ¥ > 7 + 5 ─ неравенство истинно, следовательно, вес вершины изменяется: V(5)1 = 12,
- V(5) > V(8) + r58 ® 12 > 6 + 23 ─ неравенство ложно, следовательно, вес вершины не изменяется.
2.4. Вычислим значение веса вершины x 6, его можно найти через x 3, x 4, x 5, x 7, x 8 или x 9:
- V(6) > V(3) + r36 ® ¥ > 18 + 20 ─ неравенство истинно, следовательно, вес вершины изменяется: V(6)1 = 38,
- V(6) > V(4) + r46 ® 38 > 7 + 16 ─ неравенство истинно, следовательно, вес вершины изменяется: V(6)2 = 23,
- V(6) > V(5) + r56 ® 23 > 12 + 10 ─ неравенство истинно, следовательно, вес вершины изменяется: V(6)3 = 22,
- V(6) > V(7) + r67 ® 22 > 3 + 17 ─ неравенство истинно, следовательно, вес вершины изменяется: V(6)4 = 20,
- V(6) > V(8) + r68 ® 20 > 6 + 15 ─ неравенство ложно, следовательно, вес вершины не изменяется.
- V(6) > V(9) + r69 ® 20 > 11 + 9 ─ неравенство ложно, следовательно, вес вершины не изменяется,
3. Конец работы алгоритма.
Алгоритм Форда дает кратчайшее расстояние от вершин до фиксированной вершины, а сами цепи не определяет.
Для определения цепи от выбранной вершины до фиксированной воспользуемся равенством V(j) ─ V(i) = ri,j.
Например, найдем путь от x 6 до x 1. Ищется предпоследний шаг при пересчете индекса V(6). Это x 6 ─ x 7. Затем для x 7 определяется вершина пересчета. Это x 6 - x 1. Следовательно, кратчайший путь x 6 – x 7 ─ x 1, а – кратчайшее расстояние между вершинами x 1 и x 6 определено ранее V(6) = 20.
Пример 2. Пусть задан граф G = (X, U). Найти с помощью алгоритма Дейкстра кратчайшие пути в заданном графе G от фиксированной вершины до всех остальных.
Решение: Рассмотрим матрицу смежности графа G:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 1 | 0 | 10 | 0 | 0 | 0 | 0 | 3 | 6 | 12 | . |
| 2 | 10 | 0 | 18 | 0 | 0 | 0 | 2 | 0 | 13 | |
| 3 | 0 | 18 | 0 | 25 | 0 | 20 | 0 | 0 | 7 | |
| R=4 | 0 | 0 | 25 | 0 | 5 | 16 | 4 | 0 | 0 | |
| 5 | 0 | 0 | 0 | 5 | 0 | 10 | 0 | 23 | 0 | |
| 6 | 0 | 0 | 20 | 16 | 10 | 0 | 17 | 15 | 9 | |
| 7 | 3 | 2 | 0 | 4 | 0 | 17 | 0 | 0 | 24 | |
| 8 | 6 | 0 | 0 | 0 | 23 | 15 | 0 | 0 | 5 | |
| 9 | 12 | 13 | 7 | 0 | 0 | 9 | 24 | 5 | 0 |
Постоянные пометки будем обозначать *, остальные временные.
1°. l (x 1) = 0*. l (xi) = ¥, " xi ¹ x 1, p = x 1.
В качестве начальной вершины принимаем вершину x 1. Всем остальным вершинам графа присваиваем метки l (xi) = ¥.
Первая итерация
2°. Г(p) = Г(x 1) = { x 2, x 7, x 8, x 9}. Возьмем вершину x 2 и из выражения (15.9) получим:
l (x 2) min[ l (x 2), l (x 1) + r(x 1, x 2)] = min[¥, 0* + 10] = 10.
Аналогично вычисляем значения меток для других вершин, смежных с вершиной x 1: l (x 7) = 3, l (x 8) = 6, l (x 9) = 12.
3°. В списке вершин графа выберем вершину, имеющую минимальное значение метки: Min[ x 2, x 7, x 8, x 9, x 3, x 4, x 5, x 6] = min[10, 3, 6, 12, ¥, ¥, ¥, ¥] = 3 ─ соответствует вершине x 7.
4°. Вершина x 7 получает постоянную пометку l(x 7) = 3*, p = x 7.
5°. Не все вершины имеют постоянные пометки, переходим к п. 2°.
Вторая итерация
2°. Г(p) = Г(x 7) = { x 2, x 4, x 6, x 9} ─ все пометки временные. Из выражения (1.9) вычисляем:
l (x 2) = min[ l (x 2), l (x 7) + r(x 7, x 2)] = min[10, 3* + 2] = 5.
Аналогично l (x 4) = 7, l (x 6) = 17, l (x 9) = 12.
3°. Min[ x 2, x 4, x 6, x 8, x 9, x 3, x 5] = min[5, 7, 17, 6, 12, ¥, ¥] = 5 ─ соответствует вершине x 2.
4°. Вершина x 2 получает постоянную пометку l (x 2) = 5*, p = x 2.
5°. Перейдем к п. 2°, т.к. не все вершины имеют постоянные пометки.
Третья итерация
2°. Г(p) = Г(x 2) = { x 1, x 3, x 7, x 9}, только x 3 и x 9 имеют временные пометки. Из выражения (15.9) получим l (x 3) = min[¥, 5* + 18] = 23, l (x 9) = min[12, 5* + 13] = 12.
3°. Min[ x 3, x 4, x 8, x 6, x 9, x 5] = min[23, 7, 6, 17, 12, ¥] = 6 ─ соответствует вершине x 8.
4°. Вершина x 8 получает постоянную пометку l (x 8) = 6*, p = x 8.
5°. Перейдем к п. 2°, так как. не все вершины имеют постоянные пометки.
Четвертая итерация
2°. Г(p) = Г(x 8) = { x 9, x 6, x 5}, x 5 и x 9 имеют временные пометки. Из выражения (15.9) получим:
l (x 5) = min[¥, 6* + 23] = 29, l (x 9) = min[12, 6* + r(x 8, x 9)] = 11.
3°. Min[ x 5, x 9, x 3, x 4, x 5] = min[29, 11, 23, 7, 29] = 7 ─ соответствует вершине x 4.
4°. Вершина x 4 получает постоянную пометку l (x 4) = 7*, p = x 4.
5°. Переход к п. 2°.
Пятая итерация
2°. Г(p) = Г(x 4) = { x 3, x 6, x 5}. l (x 3) = 23, l (x 6) = 17, l (x 5) = 12.
3°. Min[ x 5, x 6, x 9, x 3] = min[12, 17, 11, 23] = 11.
4°. Вершина x 9 получает постоянную пометку l (x 9) = 11*, p = x 9.
5°. Переход к п. 2°.
Шестая итерация
2°. Г(p) = Г(x 9) = { x 3, x 6} (берем только непомеченные вершины).
(x6) = min[ l (x 6), l (x 9) + r(x 6, x 9)] = [17, 11* + 9] = 17, l (x 3) = 18.
3°. Min[ x 5, x 6, x 3] = min[12, 17, 18] = 12.
4°. Вершина x 5 получает постоянную пометку l (x 5) = 12*, p = x 5.
5°. Переход к п. 2°.
Седьмая итерация
2°. Г(p) = Г(x 5) = { x 6}.
l (x 6) = min[ l (x 6), l (x 5) + r(x 5, x 6)] = [17, 12* + 10] = 17.
3°. Min[ x 6, x 3] = min[17, 18] = 17.
4°. Вершина x 6 получает постоянную пометку l (x 6) = 17*, p = x 6.
5°. Переход к п. 2°.
Восьмая итерация.
2°. Г(p) = Г(x 3) = Æ.
l (x 3) = min[18] = 18, p = x 3. Все вершины помечены.
Итак, получили кратчайшие пути от вершины x 1 до всех остальных:
x 1 ® x 2(5*), x 1 ® x 3(18*), x 1 ® x 4(7*), x 1 ® x 5(12*), x 1 ® x 6(17*), x 1 ® x 7(3*), x 1 ® x 8(6*), x 1 ® x 9(11*);
x 1 ® x 7 ® x 2 ® x 3(18*), x 1 ® x 7 ® x 2(5*), x 1 ® x 8(6*), x 1 ® x 8 ® x 9(11*), x 1 ® x 7 ® x 6(17*), x 1 ® x 7 ® x 4 ® x 5(12*), x 1 ® x 7 ® x 4(7*).
Длину цепи, т.е. суммарную стоимость весов пройденных ребер, можно получить при помощи описанной ранее рекурсивной процедуры.
Например: x 1 ® x 3(18*), сумму 18 дает вершина x 9 с ребром { x 9 ─ x 3}:
имеем x 3 ® x 9(11*), сумму 11 дает вершина x 8 с ребром { x 8 ─ x 9}.
имеем x 3 ® x 9 ® x 8(6*), сумму 6 дает вершина x 1 с ребром { x 1 ─ x 8}.
Тогда имеем кратчайший путь x 3 ® x 9 ® x 8 ® x 1 длиной 18.
Результат построения кратчайших путей в графе G показан на рис. 15.33.
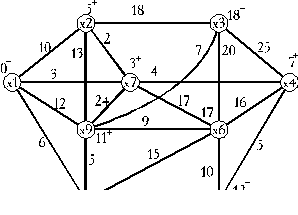
Рис. 15.33. Граф G
 2020-04-07
2020-04-07 254
254








