Вопросы для самоконтроля

1. Дайте определение и приведите примеры плоских и планарных графов.

2. Дайте определение плоской карты.

3. Запишите теорему Эйлера о плоской карте.

4. Дайте определение максимально планарного графа.

5. Приведите теоремы о планарности графов.

6. Каким образом можно связать понятия двойственности и планарности графов?

7. Какие графы являются гомеоморфными?

8. Поясните понятия толщины графа и числа скрещиваний.

9. Приведите эвристики для определения планарности графа.

10. Сформулируйте основную идею алгоритмов минимизации пересечений ребер графа.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1. Приведите примеры, подтверждающие справедливость теоремы 3.4 и ее следствий.

2. Запишите словесный алгоритм определения планарности на основе теоремы Понтрягина-Куратовского.

3. Запишите словесный алгоритм определения планарности на основе теоремы Харари-Татта.

4. Запишите словесный алгоритм определения планарности на основе теоремы Мак-Лейна.

5. Запишите словесный алгоритм определения планарности на основе теоремы Уитни.

6. Запишите словесный алгоритм определения планарности на основе теоремы Бадера.

7. Запишите словесный алгоритм определения планарности на основе циклических методов.

8. Запишите словесный алгоритм определения планарности на основе матричных методов.

9. Запишите словесный алгоритм определения планарности на основе комбинированных методов.

10. Запишите словесный алгоритм расположения полного графа на плоскости для минимизации пересечений ребер графа.

 

Планарность является важнейшим разделом теории графов. Определение планарных графов позволит строить модели объектов без пересечения ребер (связей).

Ориентированные графы

Способы задания

Часто при описании соединений в схемах необходимо учитывать направление прохождения сигнала.

Ориентированный граф будем обозначать D = (X, U) и называть графом. Ориентированным графом(орграфом) D, как уже было отмечено ранее, называется пара множеств (X(D), U(D)), где X(D) - непустое конечное множество вершин графа D, а U(D) - конечное множество упорядоченных пар элементов из X(D), называемых дугами. К примеру, дуга, первым элементом которой является вершина x_i, а вторым - вершина x_j, называется дугой из x_i в x_j.

По аналогии с неориентированными графами определим некоторые базовые понятия для ориентированных графов. Маршрутом в орграфе D называется чередующаяся последовательность ребер и дуг (x ₀, u ₁, x ₁,..., u_n, x_n), где каждая дуга U _i = (x_{i - 1}, x_i). Путь в орграфе - это маршрут, все вершины которого различны. Контур в орграфе D - это простой замкнутый маршрут, в котором совпадают только первая и последняя вершина. Если в орграфе D существует путь из вершину x_i в вершину x_j, то в этом случае говорят, что вершина x_j достижима из вершины x_i. Неориентированный граф, полученный из орграфа D путем замены всех дуг на ребра, называется основанием графа D.

Орграф D может быть однозначно задан матрицей смежности R(D) = || r_ij || _{n ´ n}, причем

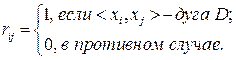
Например, пусть задан граф D, показанный на рис. 17.20.

 

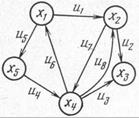
Рис. 17.20. Граф D

 

Тогда его матрица смежности R(D) имеет вид

		1	2	3	4	5	r +(xj)	.
R(D) =	1	0	1	0	0	1	2
	2	0	0	1	1	0	2
	3	0	0	0	0	0	0
	4	1	1	1	0	0	3
	5	0	0	0	1	0	1
	r –(xj)	1	2	2	2	1

 

Так как r_ij ¹ r_ji, то матрица не симметрична относительно главной диагонали. То есть в общем случае матрица смежности орграфа не будет симметрична относительно главной диагонали.

Дуга u_i = < x_i, x_j > считается положительно инцидентной ее конечной вершине x_j. Число дуг, положительно инцидентных вершине x_j (т.е. сумма единиц строки матрицы D), называется полустепенью захода и обозначается r ⁺(x_j). Число дуг, отрицательно инцидентных x_j, т.е. выходящих из x_j (сумма единиц столбца матрицы D), называется полустепенью исхода и обозначается через r ^–(x_j). Сумма вышеуказанных величин определяет локальную степень r (x_i) вершины x_i:

r (x_j) = r ⁺(x_j) + r ^–(x_j).

Так как любая дуга положительно инцидентна некоторой вершине x_j и также отрицательно инцидентна той же самой вершине x_j, то

.

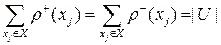Ориентированный граф D также можно задать матрицей инцидентности I(D). С учетом вышеупомянутых определений, элемент x_i матрицы инцидентности I(D) может принимать одно из трех значений:

1) элемент равен нулю, если не существует дуги, инцидентной рассматриваемой вершине (вершина не инцидентна дуге);

2) элемент равен +1, если существует дуга, исходящая из вершины;

3) элемент равен -1, если существует входящая в вершину дуга.

Для графа D на рис. 17.20 матрица инцидентности имеет вид

 

 

		u 1	u 2	u 3	u 4	u 5	u 6	u 7	u 8	.
I(D) =	х 1	+ 1	0	0	0	+ 1	- 1	0	0
	x 2	- 1	+ 1	0	0	0	0	+ 1	- 1
	х 3	1	- 1	- 1	0	0	0	0	0
	x 4	0	0	+ 1	- 1	0	+ 1	- 1	+ 1
	x 5	0	0	0	+ 1	- 1	0	0	0