Отделение корней во многих случая можно произвести графически, учитывая, что действительные корни уравнения f (x)= 0(1.1) – это есть точки пересечения графика функции y = f (x)с осью абсцисс y = 0 (рис. 1). Необходимо построить график функции y = f (x), на оси Oх отметить отрезки, содержащие по одному корню. Часто для упрощения построения графика функции y = f (x)исходное уравнение (1.1) заменяют равносильным ему уравнением:
f 1(x) - f 2(x) = 0, (2.1)
где функции f 1(x) и f 2(x) – более простые, чем функция f (x).
|


|
|



Рис. 1. Рис. 2.
Пример 1. Найти корни уравнения  .
.
Решение. Областью определения данной функции является множество  .
.
Перепишем исходное уравнение в виде 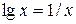 . Обозначим через f 1(x) =
. Обозначим через f 1(x) = 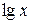 и f 2(x) =
и f 2(x) =  и построим их графики.
и построим их графики.

 у
у
f 2(x) = 

 f 1(x) =
f 1(x) = 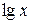
 х
х
2a 3
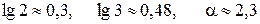 .
.
Нахождение корней таким способом упрощается, если одна из функций f 1(x) или f 2(x) – линейная.
2.2. Аналитический метод отделения корней
При отделения действительных корней аналитическим способом используют ряд теорем.
Теорема 1. Алгебраическое уравнение п -й степени
 (2.2)
(2.2)
имеет ровно п корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность, при этом аi – действительные коэффициенты, а 0 ¹ 0.
Замечания. 1) Корень a уравнения (2.2) имеет кратность s, если 
 . 2) При п > 5 (1.1) не имеет решение в формульном виде. Поэтому корни алгебраических (п > 2) и трансцендентных уравнений, как правило определяются приближённо с заданной точностью.
. 2) При п > 5 (1.1) не имеет решение в формульном виде. Поэтому корни алгебраических (п > 2) и трансцендентных уравнений, как правило определяются приближённо с заданной точностью.
Теорема 2. Если x = a + bi – корень алгебраического уравнения (2.2) кратности s, то число х = а - bi также является корнем той же кратности.
Следствие. Алгебраическое уравнение нечётной степени имеет, по крайней мере, один действительный корень.
Теорема 3. Если функция f (х), определяющая уравнение f (х) = 0, на концах отрезка [ а, b ] принимает значения разных знаков, т. е. f (а) f (b) < 0, то на этом отрезке содержится, по крайней мере, один корень уравнения. Если же f (х) непрерывна и дифференцируема и её первая производная сохраняет знак внутри отрезка [ а, b ], то на [ а, b ] находится только один корень a уравнения.
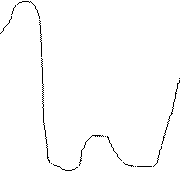


 y f (a) y
y f (a) y

 f (b)
f (b)
a1 a2 a3 b x a x
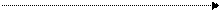


 a a b
a a b
f (b) f (a)
Замечания. 1. Для того чтобы отделить все действительные корни уравнения f (х) = 0, достаточно указать все интервалы монотонности функции f (х), так как на каждом из этих интервалов может быть не более одного корня.
2. Отделение корня считается завершенным, если указан конечный промежуток, содержащий единственный корень.
Пример 2. Отделить корни уравнения 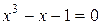 .
.
Решение. Функция  и
и  непрерывны на всей числовой оси. Определив интервалы монотонности
непрерывны на всей числовой оси. Определив интервалы монотонности  ,
,  ,
,
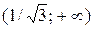 можно выделить интервал, содержащий корень. Это
можно выделить интервал, содержащий корень. Это 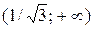 . Проверим знак функции в целочисленных точках:
. Проверим знак функции в целочисленных точках:  . Таким образом, мы определили, что
. Таким образом, мы определили, что 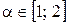 .
.
Теорема 4. (Правило Кольца). Пусть А = max  , где аk – коэффициенты уравнения (2.2.)
, где аk – коэффициенты уравнения (2.2.)  .
.
Тогда корни уравнения заключены в круговом кольце 
где  .
.
Замечание. Числа r и R являются соответственно нижней и верхней границами положительных корней уравнения (2.2). Аналогично числа – R и – r служат соответственно нижней и верхней границами отрицательных корней уравнения (2.2).
Теорема 5. (Теорема Лагранжа о верхней границе положительных корней). Пусть а 0 > 0 и аk (k ³ 1) – первый отрицательный коэффициент в последовательности а 0, а 1, ..., ап- 1, ап; с – наибольшая из абсолютных величин отрицательных коэффициентов. Тогда за верхнюю границу положительных корней уравнения (2.2) можно принять число:
 .
.
Теорема 6. (О нижних и верхних границах положительных и отрицательных корней алгебраического уравнения). Пусть K – верхняя граница положительных корней уравнения Рп (х)= 0; K 1 – верхняя граница положительных корней уравнения Рп (- х)= 0; K 2 – верхняя граница положительных корней уравнения хп × Рп  = 0; K 3 – верхняя граница положительных корней уравнения хп × Рп
= 0; K 3 – верхняя граница положительных корней уравнения хп × Рп 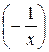 = 0. Тогда положительные корни
= 0. Тогда положительные корни  и отрицательные корни
и отрицательные корни  уравнения (2.2) удовлетворяют неравенствам:
уравнения (2.2) удовлетворяют неравенствам:
 .
.
Теорема 7. (Теорема Декарта). Число s 1положительных корней (с учётом их кратностей) алгебраического уравнения Рп (х)= 0 равно числу перемен знаков в последовательности коэффициентов а 0, а 1, ..., ап- 1, ап или меньше этого числа на чётное число, а число s 2отрицательных корней – числу постоянств знака в этой последовательности или меньше этого числа на чётное число (коэффициенты, равные нулю, не учитываются).
Теорема 8. (Теорема Гюа о необходимом признаке действительности всех корней алгебраического уравнения). Если алгебраическое уравнение (2.2) имеет все действительные корни, то квадрат каждого не крайнего коэффициента больше произведения двух его соседних коэффициентов, т.е. выполняется неравенство
 (k = 1, 2,..., п - 1).
(k = 1, 2,..., п - 1).
Следствие. Если при каком-нибудь k выполнено неравенство 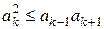 , то уравнение (2.2) имеет, по крайней мере, одну пару комплексных корней.
, то уравнение (2.2) имеет, по крайней мере, одну пару комплексных корней.
Теорема 9. (Оценка погрешности приближенного корня). Пусть А – точный, а a – приближенный корни уравнения f (х) = 0, находящиеся на одном и том же отрезке [ а, b ], причем  при х Î [ а, b ], тогда
при х Î [ а, b ], тогда 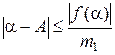 .
.
В частности за т 1 можно взять наименьшее значение 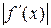 при х Î [ а, b ].
при х Î [ а, b ].
Доказательство. Применяя теорему Лагранжа, имеем
 ,
,
где с Î  , т.е. с Î [ а, b ].
, т.е. с Î [ а, b ].
Т.к.  и
и 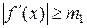 , то
, то 
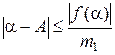 .
.
Пример 3. Определить число положительных и отрицательных корней, а также их границы для уравнения: 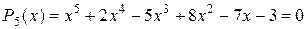 .
.
Решение. п = 5 Þ уравнение имеет пять корней, из них по крайней мере один действительный, так как степень уравнения нечетная.
Правило кольца.  .
.
 .
.
Теорема Лагранжа. Т.к. а 2 = -5 – первый отрицательный коэффициент в последовательности 1, 2, -5, 8, -7, -3, то k = 2, а 0 = 1, с = 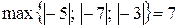 . Следовательно
. Следовательно
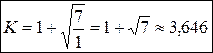 .
.
Теорема о верхних и нижних границах положительных и отрицательных корней.
Найдем верхнюю границу K 1положительных корней уравнения Р (- х) = 0:
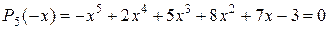 .
.
Т.к. старший коэффициент должен быть положительным, то
 .
.
Для этого уравнения k = 1, а 0 = 1, с = 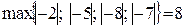 . Следовательно
. Следовательно
 .
.
Найдем верхнюю границу K 2положительных корней уравнения 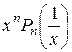 = 0:
= 0:
 .
.
Для этого уравнения k = 2, а 0 = 3, с =  . Следовательно
. Следовательно
 .
.
Найдем верхнюю границу K положительных корней уравнения 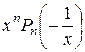 = 0:
= 0:

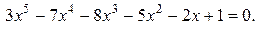
Для этого уравнения k = 1, а 0 = 3, с = 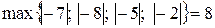 . Следовательно
. Следовательно
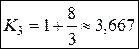 .
.
Тогда 
Или 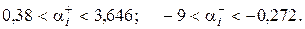
Теорема Декарта. Р 5(х): 1, 2, -5, 8, -7, -3 имеет три перемены и два постоянства знака, т.е. S 1 = 3, S 2 = 2 Þ число положительных корней 3 или 1, отрицательных корней 2 либо 0.
Теорема Гюа. Т.к. квадрат каждого ненулевого коэффициента больше произведения его соседних коэффициентов, то необходимый признак действительности всех корней выполняется.
Пример 4. Отделить число положительных и отрицательных корней, их границы для уравнения 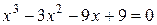 .
.
Решение. Уравнение имеет три корня, среди которых, по крайней мере, один действительный. Р 3(х): 1, -1, -9, 9 имеет две перемены и одно постоянства знака, т.е. возможно два или ни одного положительного корня и один отрицательный корень. Т.к. теорема Гюа выполняется, то имеем три действительных корня.
По теореме 3 имеем  ,
,
 .
.
Таким образом, интервалы монотонности  .
.
+ -1 - 3 +
 |
Итак, уравнение имеет три действительных корня на интервалах монотонности 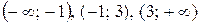 . Первый и третий интервалы бесконечные. Чтобы сделать их конечными, воспользуемся правилом кольца: А = 9, В = 9, тогда r =1/2, R = 10 и
. Первый и третий интервалы бесконечные. Чтобы сделать их конечными, воспользуемся правилом кольца: А = 9, В = 9, тогда r =1/2, R = 10 и  . Т.к. у нас два положительных и один отрицательный корень, то получим
. Т.к. у нас два положительных и один отрицательный корень, то получим  . Проверим знаки функции на концах отрезков:
. Проверим знаки функции на концах отрезков:
 .
.
Ответ:  .
.
 2020-04-07
2020-04-07 641
641







