2020-04-07
139
Один из критериев, которые мы могли бы применить для подходящей линии регрессии на диаграмме рассеяния, основан на выборе линии, для которой сумма квадратов погрешностей будет минимальна.
Близость точек рассеяния к прямой измеряется ординатами отрезков. Отклонения этих точек могут быть положительными и отрицательными, но сумма квадратов отклонений теоретической прямой от экспериментальной всегда положительна и должна быть минимальна. Факт несовпадения всех точек рассеяния с положением линии регрессии указывает на существование расхождения между экспериментальными и теоретическими данными. Таким образом, можно сказать, что никакая другая линия регрессии, кроме той, которую нашли, не может дать меньшую сумму отклонений между экспериментальными и опытными данными. Следовательно, найдя теоретическое уравнение ý и линию регрессии, мы удовлетворяем требованию наименьших квадратов.
Это делается с помощью уравнения связи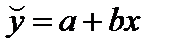 
, используя формулы для нахождения параметров а и b. Взяв теоретическое значение 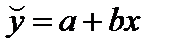и обозначив левую часть уравнения через f, получим функцию 
от неизвестных параметров а и b. Значения а и b будут удовлетворять минимуму функции f и находятся из уравнений частных производных 
и 
. Это необходимое условие, однако для положительной квадратической функции это является и достаточным условием для нахождения а и b.
Выведем из уравнений частных производных формулы параметров а и b:
получим систему уравнений:
где 
– среднеарифметические погрешности.
Подставив числовые значения, найдем параметры а и b.
Существует понятие 
. Это коэффициент аппроксимации.
Если е < 33%, то модель приемлема для дальнейшего анализа;
Если е > 33%, то берём гиперболу, параболу и т.д. Это даёт право для анализа в различных ситуациях.
Вывод: по критерию коэффициента аппроксимации наиболее подходящей является та линия, для которых
, и никакая другая линия регрессии для нашей задачи не даёт минимум отклонений.
