2020-04-12
107
Дизъюнктивные и конъюнктивные нормальные формы ДНФ, КНФ
Нормальная форма – это синтаксически однозначный способ записи формулы, реализующей данную функцию.
Формулу называют элементарной конъюнкцией, если она является конъюнкцией переменных и отрицаний переменных. Например, формулы 
, 
, 
, 
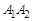– элементарные конъюнкции.
Формулу, представляющую собой дизъюнкцию (возможно одночленную) элементарных конъюнкций, называют дизъюнктивной нормальной формой (д. н. ф.). Например, формулы 
, 
, 
.
Теорема 4.1. (о приведении к ДНФ). Для любой формулы 
можно найти равносильную ей формулу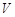 
, являющуюся ДНФ.
Формулу называют элементарной дизъюнкцией, если она является дизъюнкцией переменных и отрицаний переменных. Например, формулы 
, 
, 
и т.д.
ПРИМЕР.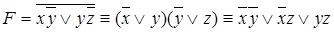 
Такая форма называется дизъюнктивной нормальной формой (ДНФ). Отдельный элемент ДНФ называется элементарной конъюнкцией или конституентой единицы.
Формулу, являющуюся конъюнкцией (возможно одночленной) элементарных дизъюнкций, называют конъюнктивной нормальной формой (КНФ). Например, формулы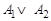 
, 
.
|
|
|
Теорема 4.2. (о приведении к КНФ). Для любой формулы можно найти равносильную ей формулу 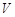, являющуюся КНФ.
ПРИМЕР. 
