1. Выражение из произвольной формы приводится к СДНФ.
2. Выполнив в СДНФ все возможные неполные склеивания, а затем все возможные поглощения мы получим Сокращенную ДНФ (СкДНФ). Конъюнкции в СкДНФ называются импликантами.
 3. На основании СкДНФ и СДНФ строим импликантную матрицу и путем нахождения минимального покрытия этой матрицы получаем минимальную дизъюнктивную нормальную форму (МДНФ).
3. На основании СкДНФ и СДНФ строим импликантную матрицу и путем нахождения минимального покрытия этой матрицы получаем минимальную дизъюнктивную нормальную форму (МДНФ).
ПРИМЕР.Минимизировать функцию 
Решение. Воспользуемся алгоритмом метода Квайна.
1. Получить СДНФ.
2. Получить сокращенную ДНФ (СкДНФ), используя следующие равносильности:
 – склеивание;
– склеивание;
 – неполное склеивание;
– неполное склеивание;
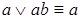 – поглощение.
– поглощение.
3. Построить импликантную матрицу, с помощью которой получить МДНФ.
1.  - ДНФ
- ДНФ
 - СДНФ
- СДНФ
1 2 3 4 5 6
2. Применяя операции склеивания, получаем СкДНФ.
| 1-2: | 
| 3-4: | 
|
| 1-5: | 
| 4-6: | 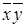
|
| 2-3: | 
| 5-6: | 
|
3. Составляем импликантную матрицу

| 
| 
| 
| 
| 
| |

| + | + | ||||

| + | + | ||||

| + | + | ||||
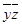
| + | + | ||||

| + | + | ||||

| + | + |
Выбираем импликанты, которые поглощают все конституенты единицы.

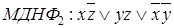
 2020-04-12
2020-04-12 157
157







