| И 1.52 | Определение 1. Изображение электрической цепи, в котором все ее узлы соединены линиями, заменяющими ветви цепи, называется графом. |
Комментарий к определению 1. Граф не несет никакой информации об элементах, содержащихся в ветвях цепи. Граф сохраняет все узлы, ветви и контуры цепи, он используется для изучения структуры электрической цепи.
| И 1.53 | Определение 2. Если в электрической цепи имеется N узлов, то любые N-1 узлов образуют систему независимых узлов (или фундаментальную систему узлов) в том смысле, что к N-1 узлам присоединены все ветви цепи. |
Комментарий к определению 2. Список независимых узлов с перечнем ветвей, присоединенных к каждому из них, полностью характеризует структуру электрической цепи (способ соединения ее ветвей).
| И 1.54 | Алгоритм выбора контуров в электрической цепи. Пусть в цепи найден какой-либо контур и разомкнут удалением из него какой-либо ветви так, чтобы целостность (связанность) цепи не нарушилась. Эту процедуру можно продолжать до тех пор, пока в оставшейся части цепи не останется ни одного контура. |
| И 1.55 | Определение 3. Все контуры, выбранные (и разомкнутые) в ходе описанной процедуры, образуют систему независимых контуров, или фундаментальную систему контуров. |
Комментарий к алгоритму построения системы независимых контуров. Построение системы независимых контуров удобно выполнить с помощью графа цепи. На рис. 1.15 показан последовательный выбор трех кнтуров в графе и их размыкание удаление одной из ветвей. Контур указан стрелкой, показывающей направление его обхода. Удаляемая ветвь отмечена крестиком. Часть графа, оставшаяся после размыкания всех трех независимых контуров, показана на рис. 1.16.

|

|

|
Рис. 1.15. Выбор системы независимых контуров
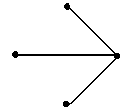
Рис. 1.16. Дерево графа
Комментарий к определению 3. Как бы ни выбирались контуры фундаментальной системы, в них войдут все ветви цепи. Список независимых контуров с перечнем ветвей, входящих в каждый из них, полностью характеризует структуру электрической цепи.
| И 1.56 | Определение 4. После размыкания всех контуров графа (в процессе построения системы независимых контуров) остается часть графа, которая называется его деревом. |
Комментарий к определению 4. Если граф содержит не менее двух узлов и не менее одного контура, то по нему можно построить несколько разных деревьев. На рис. 1.16 и 1.17 показаны два дерева, которые получаются из исходного графа на рис. 1.15.

Рис. 1.17. Дерево графа
 2020-04-12
2020-04-12 160
160








