
 Y Определение WX для прямоугольника
Y Определение WX для прямоугольника
h 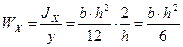

x
b
Определение WX для круга

 Y
Y
d  ;
;  ;
; 
Задача 1
Определить допускаемую величину силы F, если  . Сечение балки прямоугольное h=6см, b=4см.
. Сечение балки прямоугольное h=6см, b=4см.

|
F
 A B h
A B h
l/2 l/2 b
F/2
┼
▬
F/2
F· l /4
┼
Совместное действие изгиба и кручения
 ;
; 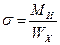
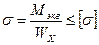
3-я гипотеза 
4-я гипотеза 
Задача 1
На вал, приводимый в движение насажен посередине шкив весом 5кН Ø1,2м. Натяжение ведущей части ремня, надетого на шкив, равно 600кг, а ведомого 300кг. [σ]=500кг/см2.
|
 | |||
 | |||
D
d
T2
0,60,6
Решение

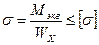
По третьей гипотезе  тогда
тогда 

|

F∑
G
RA F RB
A B
0,6 0,6
┼ 515
515
309кгм
┼
Расчет сжатых стержней на устойчивость
(продольный изгиб)
Устойчивость- способность конструкции сохранять первоначальную форму упругого равновесия.
Наименьшее значение сжимающей силы, при котором сжатый стержень теряет способность сохранять прямолинейную форму равновесия, называется критической силой Fкр.

Jmin - минимальный осевой момент сечения.
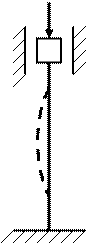 l - длина стержня. F
l - длина стержня. F
 μ – коэффициент закрепления.
μ – коэффициент закрепления.

 F F F
F F F
 |
μ=2 μ=1 μ=0,7 μ=0,5
Коэффициент запаса устойчивости 
 ; где
; где  , откуда
, откуда 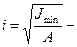 радиус инерции сечения.
радиус инерции сечения.
 гибкость стержня (величина безразмерная.
гибкость стержня (величина безразмерная.
Формула Эйлера справедлива в пределах закона Гука.
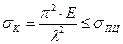 здесь σПЦ- предел пропорциональности материала стержня.
здесь σПЦ- предел пропорциональности материала стержня.

 Предел применения формулы Эйлера
Предел применения формулы Эйлера 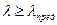
Формула Тетмайера – Ясинского (для стальных, дюралюминиевых и деревянных стержней):

где a и b – эмпирические коэффициенты, имеющие размерность напряжения. Для чугунных стержней 
Эмпирические формулы Тетмайера – Ясинского применимы при

Где λ0 – значение гибкости, при которой критическое напряжение становится равным пределу текучести (для стальных и дюралюминиевых стержней).
Для чугунных стержней условие применимости эмпирической формулы также выражается неравенством  значения
значения  и
и 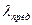 приведены в таблице.
приведены в таблице.
| Материал | a Н/мм2 | b Н/мм2 | λ0 | λпред |
| Сталь 10, Ст2………………………….. Сталь 15, Ст3………………………….. Сталь 25, Ст5………………………….. Сталь 10Г2СД, 15ГС…………………. Дюралюминий Д16Т…………………. Сосна, ель……………………………... Чугун………………………………….. | 264 310 350 429 406 29,3 - | 0,70 1,14 1,15 1,52 2,83 0,194 - | 62 61 57 50 30 - 10 | 105 100 92 83 53 70 80 |
Стальные и деревянные стержни строительных конструкций, а также сжатые стержни металлоконструкций подъемно – транспортных машин рассчитывают по формуле
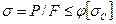 ,
,
где F – площадь поперечного сечения стержня; φ – коэффициент продольного изгиба; [σс] – основное допускаемое напряжение на сжатие, устанавливаемое без учета опасности продольного изгиба.
Коэффициент φ зависит от материала и гибкости стержня, Последняя при проектном расчете неизвестна, поэтому его приходится вести последовательными приближениями.
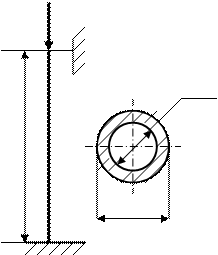 Задача 1
Задача 1
|
d=40
l=1700
D=50
Для определения гибкости рассчитываемой стойки вычисляем геометрические характеристики ее поперечного сечения:

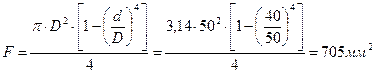
 .
.
Определим гибкость стойки:
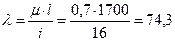 и убеждаемся, что
и убеждаемся, что  , т.е. критическую силу можно определить по формуле Эйлера:
, т.е. критическую силу можно определить по формуле Эйлера:
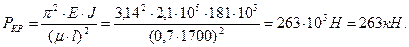
Вычисляем расчетный (действительный) коэффициент запаса устойчивости:

Таким образом,  на 5,2%
на 5,2%
 |
Задача 2
|
Y Z0
l=9м Х
№10 b
ты инерции сечения, принимая исходные геометрические характеристики по ГОСТ 8240-72;


Таким образом,  и
и 
Площадь сечения 
Минимальный радиус инерции 
Гибкость стойки (при μ=0,5) 
Следовательно, 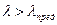 и критическую силу определяем по формуле Эйлера:
и критическую силу определяем по формуле Эйлера:

Величина допускаемой силы 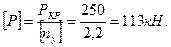
При уменьшении длины стойки вдвое критическая (и допускаемая) сила увеличится не в четыре раза, как можно было бы ожидать исходя из формулы Эйлера, а меньше. Действительно, гибкость стойки уменьшенной длины
 т.е.
т.е.  , но
, но  , и критичкское напряжение (соответственно и критическую силу) следует определять по эмпирической формуле Тетмайера – Ясинского. Применим указанную формулу, беря значения коэффициентов из таблицы
, и критичкское напряжение (соответственно и критическую силу) следует определять по эмпирической формуле Тетмайера – Ясинского. Применим указанную формулу, беря значения коэффициентов из таблицы
 .
.
Допускаемая сила 
Таким образом, величина критической и допускаемой сил возросла лишь в 1,9 раза. Это пример подтверждения того, что нельзя применять формулу Эйлера при гибкости, меньшей предельной.

|
Y 20
l=4,5м
200 20 Х
300
Так как λ<λпред, то для определения применим эмпирическую формулу

Определяем допускаемую нагрузку:

 2020-04-12
2020-04-12 193
193





 MИ=RA·0,6=515·0,6=309кгм
MИ=RA·0,6=515·0,6=309кгм



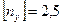 , если она изготовлена из хромоникелевой стали, для которой Е= 2,1·105Н/мм2 и σПЦ=450Н/мм2.
Решение. Для расчета на устойчивость должна быть известна критическая сила для заданной стой-ки. Необходимо установить, по какой формуле сле-дует вычислять критическую силу, т.е. надо сопоста-вить гибкость стойки с предельной гибкостью для ее материала.
Вычисляем величину предельной гибкости, так как табличных данных о λпред для материала стойки не имеется:
, если она изготовлена из хромоникелевой стали, для которой Е= 2,1·105Н/мм2 и σПЦ=450Н/мм2.
Решение. Для расчета на устойчивость должна быть известна критическая сила для заданной стой-ки. Необходимо установить, по какой формуле сле-дует вычислять критическую силу, т.е. надо сопоста-вить гибкость стойки с предельной гибкостью для ее материала.
Вычисляем величину предельной гибкости, так как табличных данных о λпред для материала стойки не имеется:

 Гибкость стойки при μ=1,0
Гибкость стойки при μ=1,0 







