 откуда
откуда
 , но
, но 
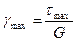 , тогда
, тогда 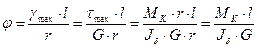
φ0 – угол закручивания, приходящийся на единицу длины [м] 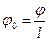
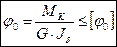
Задачи на условия жесткости при кручении:
1. Проверка жесткости 

2. Проектный расчет для круглого сплошного сечения  ,
, 

Для кольцевого сечения 
 ;
; 
Зависимость крутящего момента и мощности на валу


3. Определение допускаемой нагрузки 
ПРИМЕРЫ РЕШЕНИЯ РАСЧЕТНО-ГРАФИЧЕСКИХ ЗАДАЧ ПО ТЕМЕ
КРУЧЕНИЕ
Задача1
Для стального вала требуется:
1. Определить величины моментов, подводимых к шкиву 1 и снимаемых со шкивов 2,3,4.
2. Построить эпюру крутящих моментов на валу.
3. Определить предельный диаметр вала из расчета на прочность и жесткость, если Р2=50кВт
Р3=40кВт
Р4=30кВт
n =170 об/мин
[τ]=20МПа
[φ0]=0,25 град/м
Окончательно принимаемое значение диаметра вала должно быть округлено до ближайшего большего четного, или оканчивающегося на 5 числа (мм).
IV M2 III M1 II M3 I M4






0 2,81кНм -3,93кНм -1,68кНм 0
Определяем мощность, подаваемую на вал
Р1=Р2+Р3+Р4=50+40+30=120 (кВт)
Вращающие моменты на шкивах
 ;
; 
 ;
; 
По найденым вращающим моментам строим епюру крутячих моментов.
МКр1= -М4 = -1,68(кНм)
МКр2 = -М4-М3 = -1,68-2,25 = -3,93(кНм)
МКр3=-М4 -М3+М1= -3,93+6,74=2,81(кНм)
МКр4=-М4 -М3+М1-М2 =2,81-2,81=0
Из эпюры выбираем Mmax по модулю Mmax=MKp2=3,93(кНм)
Определяем минимальны размер вала по условию прочности
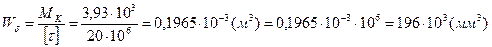

Определяем диаметр вала по условию жесткости


 Принимаем d=104мм
Принимаем d=104мм
Задача 2
В поперечном сечении полого вала возникает крутящий момент МК=6000Нм. с=d/D=0,8. [τ]=50МПа.
Найти диаметр вала по условию прочности и экономию веса по сравнению со сплошным валом в тех же условиях.
Решение
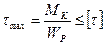
 ;
;


 где
где 



ИЗГИБ
Прямым чистым изгибом называется вид деформации, при котором в поперечных сечениях стержней возникает один внутренний силовой фактор -изгибающий момент.
Прямым поперечным изгибом называется вид деформации при котором в поперечных сечениях возникают два внутренних силовых фактора: поперечная сила и изгибающий момент.
Стержни, работающие на изгиб, называются балками.
Эпюры поперечных сил- диаграммы изменения поперечных сил по длине балки.
Эпюры изгибающих моментов- диаграммы изменения изгибающих моментов по длине балки.
Поперечная сила в сечении численно равна алгебраической сумме проекций на вертикальную ось всех внешних сил, действующих по одну сторону от рассматриваемого сечения.
Правило знаков
Поперечная сила в сечении балки mn считается положительной, если
равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа- сверху вниз(а), и отрицательной в противоположном случае (б)
 Qmn>0 F F Qmn<0
Qmn>0 F F Qmn<0
m m
+ -
F n n F
а) б)
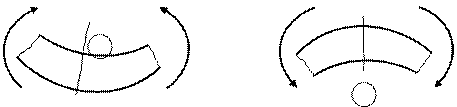
Изгибающий момент в сечении балки mn, считается положительным, если равнодействующий момент внешних сил слева от сечения направлен по часовой стрелке, а справа - против часовой стрелки (а), и отрицательным – в противоположном случае (б). При сжатии верхних волокон и растяжении нижних волокон балки моменты положительные, при сжатии нижних волокон и растяжении верхних волокон моменты отрицательные.
 | |||
 | |||
М Mmn>0 M M Mmn<0 M
m m
+
n
n -
а) б)
ПОРЯДОК ПОСТРОЕНИЯ ЭПЮР Q И MИ
1. Определяем опорные реакции.
2. Разбиваем балку на участки, границами которых являются начало, конец балки, точки приложения сосредоточенных сил, начало и конец равномерно распределенной нагрузки, пары сил.
3. Составляем уравнения для поперечных сил каждого участка, пользуясь вышеуказанным правилом.
4. Если поперечная сила плавно изменяясь проходит через нулевое значение, то необходимо определить абсциссу этого сечения, где Q обращается в «0».
5. Применяя метод сечений, записываем уравнение изгибающего момента для каждого участка. Вычисляем значение изгибающего момента в характерных точках, учитывая и точку, где Q=0.
6. По данным значениям строим эпюры поперечных сил и изгибающих моментов.
ПОРЯДОК КОНТРОЛЯ ПОСТРОЕНЫХ ЭПЮР.
1. Если участок не загружен равномерно распределенной нагрузкой, то поперечная сила постоянна, а изгибающий момент изменяется по линейному закону.
2. Если на данном участке поперечная сила равна «0», то изгибающий момент постоянный.
3. На участках, загруженных равномерно распределенной нагрузкой, Q изменяется по линейному закону, а Ми по параболе, выпуклость которой направлена навстречу нагрузке.
4. В точках приложения сосредоточенных сил на эпюре Q имеют место скачки, равные величинам приложенных внешних сил, а на эпюре изгибающих моментов – переломы, направленные навстречу силам.
5. В точке приложения пар сил на эпюре Ми – скачки, равные по величине приложенной паре сил.
6. В точках, где поперечная сила обращается в «0», Ми принимает экстремальные значения (max, min)/
7. Если рассматривать эпюры слева направо и на данном участке Q>0, то изгибающий момент будет возрастать, если Q<0, Ми будет убывать.
Дифференциальная зависимость между Ми ,Q и q
 ;
; 
Пример построения эпюр
Задача 1
 |
 F1=5кН М=1кН·м
F1=5кН М=1кН·м
I II
Z1 F2=7кН
Z2
3м 4м
2
┼ Q
▬ -5
▬ ▬ -8 M и
-15
Задача 2
|
 RA F=12кН М=8кНм RB
RA F=12кН М=8кНм RB
I II III
Z1 Z2
Z3
1м 1,5м 1,5м
11
┼
▬ Q
1
11
9,5
┼ ┼
1,5
┼ Mи
Задача 3
 |

|
z1 z2
Z3
F=20кН
1м 3м 1м
3,5м
20
┼ ┼
Q
45 4
44
┼ 40
MИ
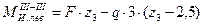
4≤z3≤5; z3=4→M=44кНм; z3=5→M=40кНм
Условия прочности при изгибе
| ||||
 | ||||
О О1
М М
О О1
σ1
σ2
σ3
σ4

|

σ
θ
 δ
δ
O
О О1
A A1
y



Самыми рациональными сечениями при изгибе являются двутавр и швеллер
 | ||
 | ||
Y σ – перпендикулярно площадке
σ dA 
y х
здесь  и
и 

 , здесь WX – осевой момент сопротивления сечения
, здесь WX – осевой момент сопротивления сечения
 (см3, мм3)
(см3, мм3) 
На условие прочности при изгибе решаются задачи:
 2020-04-12
2020-04-12 208
208

 ;
; 
 ;
; 


 ;
; 

 0≤z1≤1
z1=0→M=0; z1=1→M=RA·1=11кНм
0≤z1≤1
z1=0→M=0; z1=1→M=RA·1=11кНм
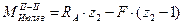 1≤z2≤2,5
Z2=1→M=11·1=11кНм
Z2=2,5→M=11·2,5=9,5кНм
1≤z2≤2,5
Z2=1→M=11·1=11кНм
Z2=2,5→M=11·2,5=9,5кНм
 ;
2,5≤z3≤4
Z3=2,5→M=11·2,5-12·1,5=1,5кНм
Z3=4 →M=11·4-12·3-8=0
;
2,5≤z3≤4
Z3=2,5→M=11·2,5-12·1,5=1,5кНм
Z3=4 →M=11·4-12·3-8=0

 1≤z2≤4
z2=1→
1≤z2≤4
z2=1→  z2=4→
z2=4→  Определяем абсциссу пересечения линии Q с нулевой линией
Определяем абсциссу пересечения линии Q с нулевой линией
 ; 20+8=8z2; z2=3,5м.
; 20+8=8z2; z2=3,5м.

 0≤z1≤1
z1=0→M=0; z1=1→M=20(кН)
0≤z1≤1
z1=0→M=0; z1=1→M=20(кН)
 1≤z2≤4
1≤z2≤4
 →M=20кНм; z2=4→M=44кНм
z2=2,5→M=45кНм
→M=20кНм; z2=4→M=44кНм
z2=2,5→M=45кНм







