ФПР1
6.1. Отображение и преобразование множеств. Преобразование плоскости. Группы преобразований. Подгруппы группы преобразований.
Пусть X и Y – непустые множества. Говорят, что задано отображение f множества X во множество Y, если каждому элементу 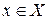 поставлен в соответствие определенный элемент
поставлен в соответствие определенный элемент 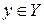 . Если дано некоторое отображение
. Если дано некоторое отображение 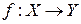 , то элемент y=f (x) называется образом элемента
, то элемент y=f (x) называется образом элемента 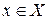 , а х – прообразом элемента
, а х – прообразом элемента 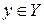 .
.
Если для любых двух различных элементов 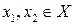 выполнено
выполнено 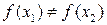 , то отображение f называется инъективным отображением или инъекцией. Если f (X)= Y, т.е. для любого элемента y из Y существует
, то отображение f называется инъективным отображением или инъекцией. Если f (X)= Y, т.е. для любого элемента y из Y существует 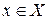 такой, что f (x)= y, то отображение f называется сюръективным отображением (сюръекцией). Если отображение
такой, что f (x)= y, то отображение f называется сюръективным отображением (сюръекцией). Если отображение 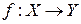 одновременно является инъективным и сюръективным, то оно называется взаимно однозначным отображением множества X на множество Y или биективным отображением (биекцией).
одновременно является инъективным и сюръективным, то оно называется взаимно однозначным отображением множества X на множество Y или биективным отображением (биекцией).
Если 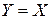 , то отображение
, то отображение 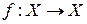 называется отображением множества Х на себя. Любое биективное отображение множества Х на себя называется преобразованием множества Х.
называется отображением множества Х на себя. Любое биективное отображение множества Х на себя называется преобразованием множества Х.
Обозначим 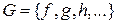 - множество всех преобразований множества Х. Введем на множестве G операцию композиции преобразований следующим образом. Пусть
- множество всех преобразований множества Х. Введем на множестве G операцию композиции преобразований следующим образом. Пусть 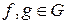 . Каждому элементу
. Каждому элементу 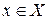 поставим в соответствие элемент z такой, что y=f (x), z=g (y), тогда z=g (f (x)). Таким образом, определено новое преобразование множества Х, переводящее элемент х в элемент z, которое обозначается
поставим в соответствие элемент z такой, что y=f (x), z=g (y), тогда z=g (f (x)). Таким образом, определено новое преобразование множества Х, переводящее элемент х в элемент z, которое обозначается 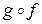 и называется композицией преобразований f и g:
и называется композицией преобразований f и g:
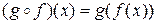 . (1)
. (1)
Преобразование 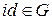 , которое каждому элементу множества Х ставит в соответствие тот же элемент, называется тождественным. Преобразование
, которое каждому элементу множества Х ставит в соответствие тот же элемент, называется тождественным. Преобразование 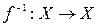 называется обратным преобразованию
называется обратным преобразованию 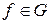 , если
, если 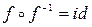 .
.
Группой называется пара 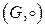 , где G – непустое множество, на котором задана бинарная операция
, где G – непустое множество, на котором задана бинарная операция 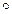 (закон композиции) и выполнены следующие три условия (аксиомы):
(закон композиции) и выполнены следующие три условия (аксиомы):
1) Операция 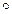 ассоциативна, т.е. для любых элементов
ассоциативна, т.е. для любых элементов 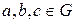 имеем:
имеем: 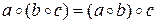 .
.
2) В множестве G существует такой элемент e (нейтральный элемент), что 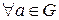 :
: 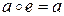 .
.
3) Для любого элемента 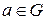 существует элемент а- 1 (обратный элемент) такой, что
существует элемент а- 1 (обратный элемент) такой, что 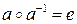 .
.
Докажем, что множество преобразований множества G образует группу относительно операции композиции преобразований, т.е. для множества G и операции композиции преобразований выполнены условия 1)-3).
1) Пусть 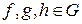 . Для любого
. Для любого 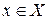 имеем по определению композиции преобразований
имеем по определению композиции преобразований
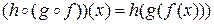 и
и 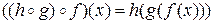 ,
,
Т.е. преобразования 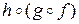 и
и 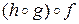 переводят элемент
переводят элемент 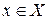 в один и тот же элемент
в один и тот же элемент 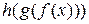 , значит, мы имеем не два преобразования, а одно
, значит, мы имеем не два преобразования, а одно
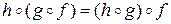 .
.
2) Положим 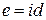 . Очевидно, из определения тождественного преобразования следует
. Очевидно, из определения тождественного преобразования следует 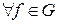 :
: 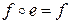 . Значит, тождественное преобразование id является нейтральным элементом.
. Значит, тождественное преобразование id является нейтральным элементом.
3) Любое преобразование 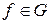 является биекцией множества Х на себя, поэтому существует обратное отображение
является биекцией множества Х на себя, поэтому существует обратное отображение 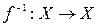 , которое является преобразованием множества G, поэтому
, которое является преобразованием множества G, поэтому 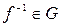 . По определению обратного отображения имеем:
. По определению обратного отображения имеем: 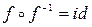 .
.
Пусть 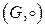 – группа и
– группа и 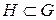 ,
, 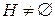 . Если
. Если 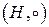 – группа, то она называется подгруппой группы
– группа, то она называется подгруппой группы 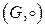 . Непустое множество Н группы G является подгруппой этой группы, если выполнены два условия:
. Непустое множество Н группы G является подгруппой этой группы, если выполнены два условия:
1) Если 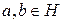 , то
, то 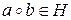 ;
;
2) Если 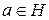 , то
, то 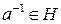 .
.
 2020-04-12
2020-04-12 874
874







