Гравитационный момент

Рассмотрим движение космического аппарата в поле тяготения некоторого небесного тела (планеты) с гравитационной постоянной .

Гравитационный момент , действующий на космический аппарат относительно его центра масс, возникает вследствие того, что центр масс и центр тяжести аппарата в общем случае не совпадают. Действительно, векторы ускорения силы тяжести в различных точках космического аппарата всегда различны, поскольку все они направлены к центру притяжения планеты, а следовательно, если рассматриваемые точки не лежат на одной прямой, идущей через центр притяжения, то векторы не параллельны, а если точки лежат на одной такой прямой, то имеют различное удаление от центра притяжения и, значит, соответствующие ускорения отличаются по величине.

Гравитационный момент для космического аппарата с тензором инерции 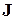 в выбранной системе координат рассчитывается по формуле [?]

,

(2)

где  – расстояние от центра масс космического аппарата до центра притяжения планеты, а  – орт местной вертикали.

В орбитальной системе орт  имеет координаты . При переходе к связанной системе координат используются элементы ,  и  второго столбца матрицы направляющих косинусов : .

В частном случае, когда космический аппарат движется по круговой орбите с угловой скоростью , а оси связанной системы координат совпадают с его главными осями инерции, формула (2) упрощается и приобретает вид

.

(3)