Поняття про визначники вищих порядків

Визначники другого і третього порядків та їхні властивості

 

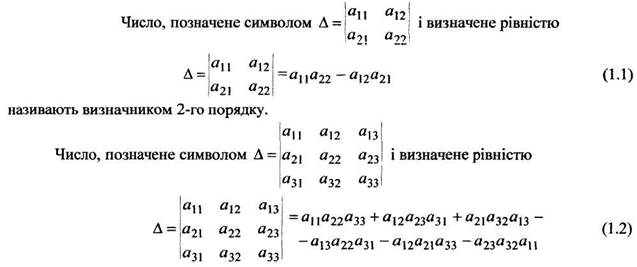
називають визначником 3-го порядку.

Числа а₁₁, а₁₂,..., а₃₃, що складають визначник, називаються елементами визначника.

Для позначення елементів визначника використовуються подвійні індекси: а_ij.

Перший індекс (i) визначає номер рядка, а 2-й (j) - номер стовпчика визначника.

Права частина рівності (1.2) обчислюється за такими схемами.

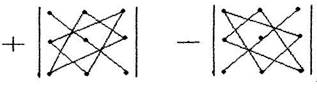
тобто елементи добутків (1.2), взяті з відповідно вказаними знаками, або з'єднані відрізками (головна і друга діагональ), або утворюють трикутники.

Для обчислення визначника третього порядку можна використовувати і так зване „правило Саррюса". Для обчислення визначника за цим правилом припишемо справа до визначника спочатку перший, а потім другий стовпчики:

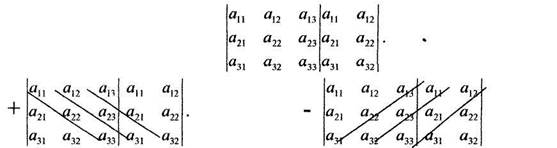
Тоді, як показано на схемі, доданки суми (1.2) що не змінюють свій знак, знаходяться шляхом добутку елементів, що стоять на головній діагоналі та паралельно їй; а для знаходження доданків, що змінюють свій знак, треба перемножити елементи, що стоять на другій діагоналі та паралельно їй.

 

Розклад визначника за елементами рядка або стовпця

Позначимо через а_ij (і, j =1,2,3) елемент визначника (1.2), який знаходиться на перетині його і -го рядка j -го стовпчика. Якщо в (1.2) викреслити i -й рядок і j -й стовпчик, то одержимо визначник 2-го порядку, який називається доповнюючим мінором елемента а_ij і позначається Мij.

Мінор Мij, взятий із знаком (-1)^l+J, називається алгебраїчним доповненням елемента а_ij і позначається А_ij, тобто

Теорема розкладу. Визначник D дорівнює сумі парних добутків всіх елементів якогось рядка або стовпчика на їх алгебраїчні доповнення.

Для визначника D із (1.2) цей розклад за елементами 1-го рядка із врахуванням (1.3) буде виглядати так:

 

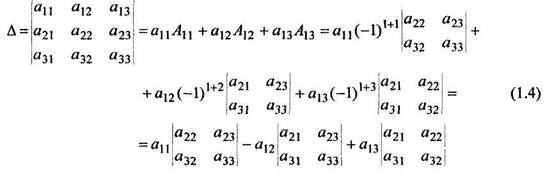
Поняття про визначники вищих порядків

Визначник п порядку дорівнює сумі добутків усіх елементів будь-якого стовпця (або рядка) на відповідні їм алгебраїчні доповнення.

У випадку використання і -го рядка це правило математично виглядає так

Цю рівність називають розкладом визначника за елементами і-го рядка.

Обчислення визначника п порядку зводиться до обчислення п визначників (п-1) порядку. Для скорочення обчислень визначник доцільно розкладати за елементами рядка або стовпця, який містить найбільшу кількість нулів. До нулів не треба знаходити алгебраїчних доповнень тому, що добуток 0 на його алгебраїчне доповнення дорівнює нулю. Властивості визначника дозволяють робити еквівалентні перетворення визначника і одержувати якомога більше нулів в деякому рядку або стовпці.

Матриці

Матрицею розміром m´n називають таблицю упорядкованих чисел або будь-яких інших об'єктів, розташованих в m рядках та п стовпцях.

Матриці позначають великими літерами, наприклад, А, В,С, та круглими дужками, а елементи матриць позначають відповідними малими літерами з двома індексами, наприклад, а_ij, b_ij, c_ij.

Перший індекс і вказує номер рядка, в якому знаходиться цей елемент, другий індекс j вказує номер стовпця,який містить цей елемент. Так, елемент С₄₃ знаходиться на перетині четвертого рядка та третього стовпця матриці С.

Матриця розміру n´1 називається матрицею-стовпцем або вектором-стовпцем.

Матриця розміру І´n називається матрицею-рядком або вектором-рядком.

Матрицю називають квадратною порядку n, якщо кількість її рядків однакова з кількістю стовпців і дорівнює п.

Нехай задані матриці

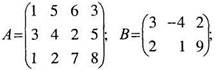
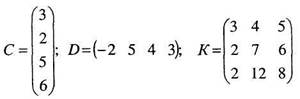
Матриця А має розмір 3´4, матриця В розміру 2´3, матриця-стовпець С розміру 4´1, D - матриця рядок розміру 1´4, матриця К - квадратна порядку 3.

Елементи квадратної матриці А порядку n, що розташовані на діагоналі матриці, яка проходить з лівого верхнього кута до правого нижнього кута, утворюють головну діагональ матриці.

Елементи квадратної матриці, що розташовані на діагоналі матриці, яка проходить з правого верхнього кута до лівого нижнього кута, утворюють неголовну (допоміжну) діагональ матриці.

Наприклад, в матриці:

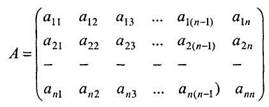 елементами головної діагоналі будуть: а₁₁, а₂₂, a₃₃,..., a_nn, a елементами неголовної діагоналі будуть: а_1n, а_2(n-1), а_3(n-1), а_n1

Квадратна матриця зветься діагональною, якщо усі її елементи дорівнюють 0, крім елементів головної діагоналі.

Діагональна матриця, усі елементи якої дорівнюють одинці, називається одиничною матрицею і позначається Е або І.

Матриці А та В називають рівними, якщо:

1. вони мають однаковий розмір;

2. їх відповідні елементи рівні, тобто а_ij = b_ij для усіх і тa j.

Якщо в матриці А рядки записати стовпцями із збереженням їх нумерації, то одержана матриця зветься транспонованою і позначається А^т, а вказана операція перетворення матриці А називається транспонуванням матриці А.

 

 

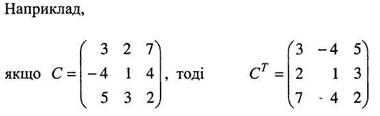
Дії над матрицями

Найпростішими діями з матрицями називають множення матриць на число, їх алгебраїчну суму та множення матриць.

Добутком матриці А на число к називається матриця, елементи якої дорівнюють добуткам відповідних елементів матриці А та числа к:

Додавати та віднімати можна лише матриці однакового розміру.

Алгебраїчною сумою матриць А та В однакового розміру m ´ п називається матриця С розміру m ´ п, елементи якої c_ij дорівнюють такої самої алгебраїчної суми елементів а_ij,; та b_ij матриць А та В:

Добуток АВ матриць А та В існує лише при виконанні умов узгодженості: кількість стовпців матриці А (першого множника) дорівнює кількості рядків матриці В (другого множника).

Добутком АВ матриці А розміру m´n матриці В розміру п´р називається матриця С розміру m´р, елементи якої c_ij дорівнюють сумі добутків елементів і -го рядка матриці А на відповідні елементи j -ro стовпця матриці В.

Таким чином, кожен елемент матриці С знаходиться за формулою:

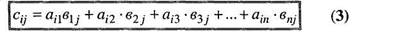
Взагалі добуток матриць не має властивості комутативності, тобто АВ#ВА. Якщо добуток двох матриць не залежить від порядку множників, тобто АВ=ВА, тоді кажуть, що ці матриці комутують.

Наприклад, якщо А - квадратна матриця порядку n, E -одинична матриця порядку п, тоді АЕ = ЕА = А.

 

Обернена матриця

Матриця А^-1 називається оберненою до матриці А, якщо виконуються рівності

Ці рівності означають, що матриці А та А^-1 комутують і їх добуток є одиничною матрицею.