Понятие множества. Подмножества

Тема: «Операции над множествами. Диаграмма Эйлера-Венна. Разбиение множества на классы»

Цель: закрепить навыки осуществления операций над множествами, навыки использования диаграмм Эйлера-Венна.

Перед началом занятия необходимо знать: понятия множества, подмножества, универсального множества, пересечения множеств, объединения множеств, разности двух множеств и дополнения; понятие диаграмм Эйлера-Венна.

После окончания занятия необходимо уметь: находить пересечение, объединение, разность и дополнение множеств, в том числе с использованием диаграмм Эйлера-Венна.

Литература:

1. Григорьев С.Г. Математика: учебник для студентов сред. проф. учреждений / С.Г. Григорьев, С.В. Иволгина; под ред. В.А. Гусева. – 6-е изд., стер. – М.: Издательский центр «Академия», 2012. – 414 с.

2. Пехлецкий И.Д.Математика: учебник для студ. образоват. учреждений сред. проф. образования/ И.Д. Пехлецкий.-10-е изд., стер.-М.: Издательский центр»Академия», 2013.-304с

3. http://diskra.ru/reshenie_zadach/?lesson=1&id=1

4. http://www.grandars.ru/student/vysshaya-matematika/mnozhestvo.html

 

Изучить теоретический материал и разобрать примеры.

Основные теоретические положения и примеры решения типовых заданий.

Понятие множества. Подмножества.

Понятие множества относится к аксиоматическим понятиям математики.

Множество – совокупность определённых, различимых между собой объектов, рассматриваемых как единое целое, и обладающая некоторым общим свойством.

Имеется три важных момента, характеризующих понятие множества:

1) объекты, входящие во множество, определённые – т.е. для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет;

2) объекты, входящие во множество, различимы между собой – т.е. во множестве не может быть двух или более одинаковых объектов;

3) все объекты, входящие во множество, мыслятся как единое целое – т.е. во множестве абстрагируются от свойств отдельных объектов, но говорят об общем свойстве множества, как единого целого; такое общее свойство называют характеристическим.

Например, можно говорить о множестве всех книг данной библиотеки, множестве всех вершин данного многоугольника, множестве всех натуральных чисел, множестве всех точек данной прямой.

Множества обозначаются прописными буквами латинского алфавита: A, B, C, D и т.д. Объекты, входящие во множество, называют элементами.

Например:

 – множество букв русского алфавита;

 – множество натуральных чисел;

– множество студентов, сидящих на 1-м ряду.

Множество, состоящее из конечного числа элементов, называется конечным, в противном случае множество называется бесконечным. Множество может содержать и всего лишь один элемент. Множество, не содержащее элементов, называется     пустым и обозначается ∅.

Множества А и S₁, рассмотренные выше, – конечные, а множество N – бесконечное.

Принадлежность элемента множеству записывается значком ∈. Например:

 – буква «бэ» принадлежит множеству букв русского алфавита;

 – буква «бета» не принадлежит множеству букв русского алфавита;

 – число 5 принадлежит множеству натуральных чисел;

 – число 5,5 – не принадлежит множеству натуральных чисел;

 – Вольдемар не сидит в первом ряду.

Таким образом, если множество содержит конечное число элементов, то оно может быть задано перечислением его элементов. Множество может быть также задано при помощи правила, позволяющего определить, является ли данный объект элементом множества или нет. При записи правило, задающее множество, отделяется вертикальной чертой или двоеточием.

Например,

1) 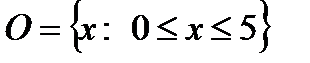 - множество чисел, принадлежащих отрезку (подразумевается множество действительных чисел, которые перечислить через запятую уже невозможно);

2) 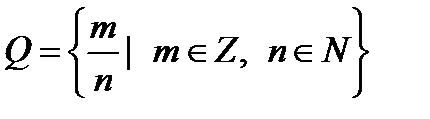- множество рациональных чисел, то есть, чисел, представимых в виде дроби  с целым числителем и натуральным знаменателем.

Множество В называется подмножеством множества А, если каждый элемент множества В одновременно является элементом множества А. Иными словами, множество В содержится во множестве А: . Значок  называют значком включения.

Например:

1)  А – это множество букв русского алфавита. Обозначим через С – множество его гласных букв, которое будет подмножеством множества А. Тогда: .

2) Пусть заданы множества А = {1, 3, 5, 7} и B = {3, 5}. Очевидно, что В есть подмножество А, т.е. .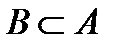

3) Множество N натуральных чисел является подмножеством множества Z целых чисел, т. е. .

4)

Из определения подмножества следует, что любое множество является подмножеством самого себя, т. е. справедливо утвержде­ние . Говорят, что А – самое широкое подмножество А. Пустое множество является подмножеством любого множества. Пустое множество является самым узким подмножеством любого множества.

Пример 1. Дано некоторое множество, состоящее из трёх элементов: . Найти все его под­множества.

Решение.

Во-первых, это – пустое множество ∅. Во-вторых, множества, содержащие по одному элементу: {а}, {b},{с}. В-третьих, множества, содержащие по два элемента: {а, b}, {b, с}, {а, с}. И, наконец, само множество {а, b, с}.

Ответ: ∅, {а}, {b},{с},{а, b}, {b, с}, {а, с},{а, b, с}.

 

Зафиксированное каким-либо образом множество объектов, допустимых при данном рассмотрении, называют универсальным множеством (базовым множеством, основным множеством, универсумом). Часто обозначается U.

Множества А и В считаются равными, если они состоят из одних и тех же элементов. Равенство множеств обозначают так: А = В.