2020-04-12
90
Влияние некоторых факторов, определяющих вариацию признаков, можно установить с помощью группировок, образовав более однородные совокупности единиц наблюдения с меньшей вариацией.
Сила влияния группировочного фактора оценивается на основе сравнения дисперсий результативного признака в выделенных группах и общей дисперсией, вычисленной до группировки.
Если исследуемую совокупность разделить на группы по факторному признаку, то для этих групп рассчитываются такие виды дисперсий: общая, межгрупповая и внутригрупповая.
Дисперсионный анализ групп включает:
1. Вычисление общей дисперсии результативного признака до группировки.
; 
.
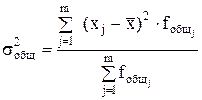2. Разделение единиц наблюдения исследуемой совокупности на группы i=1,2…n по факторному признаку.
3. Вычисление средних и дисперсий в каждой группе:
; 
.
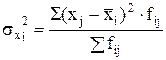4. Вычисление межгрупповой дисперсии:
.
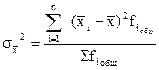Межгрупповая дисперсия отражает вариацию, возникающую под влиянием факторного признака, положенного в основу группировки. Она характеризует колеблемость групповых средних относительно общей средней.
5. Вычисление внутригрупповой дисперсии (средней величины групповых дисперсий):
.
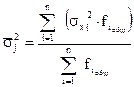Внутригрупповая дисперсия характеризует случайную вариацию в каждой отдельной группе. Эта вариация возникает под влиянием не учитываемых факторов и не зависит от признака, положенного в основу группировки.
6. Контрольная проверка:
– правило сложения дисперсий
7. Анализ качества группировок
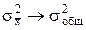и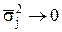 
.
В этом случае фактор, положенный в основу группировки, выбран правильно, вариация результативного признака в группах существенно уменьшилась.
8. Корреляционное отношение показывает тесноту связи между факторным и результативным признаками.
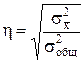
При качественной группировке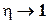 
, т.к. .
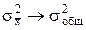при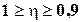 
имеет место очень сильное влияние группировочного признака;
при 
имеет место сильное влияние;
при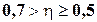 
имеет место слабое влияние;
при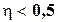 
влияние отсутствует.
Пример. Распределение численности по уровню ЗП в цехе № 1
| Дневная ЗП рабочих, д.ед. | число рабочих цеха №1, чел. (f1j) | xj, д.ед. | xj*f1j |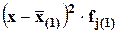 
|
| 8-10 | 2 | 9 | 18 | 91,13 |
| 10-12 | 3 | 11 | 33 | 67,69 |
| 12-14 | 5 | 13 | 65 | 37,81 |
| 14-16 | 11 | 15 | 165 | 6,19 |
| 16-18 | 10 | 17 | 170 | 15,63 |
| 18-20 | 5 | 19 | 95 | 52,81 |
| 20-22 | 4 | 21 | 84 | 110,25 |
| Итого | 40 | - | 630 | 381,5 |
1) средняя ЗП в цехе №1:
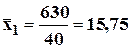д.ед.
2) групповая дисперсия в цехе №1:
Распределение численности по уровню ЗП в цехе № 2
| Дневная ЗП рабочих, д.ед. | число рабочих цеха №2, чел. (f2j) | xj, д.ед. | xj*f2j |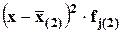 
|
| 8-10 | 6 | 9 | 54 | 158,69 |
| 10-12 | 5 | 11 | 55 | 49,39 |
| 12-14 | 6 | 13 | 78 | 7,84 |
| 14-16 | 9 | 15 | 135 | 6,61 |
| 16-18 | 3 | 17 | 51 | 24,49 |
| 18-20 | 2 | 19 | 38 | 47,18 |
| 20-22 | 4 | 21 | 84 | 188,08 |
| Итого | 35 | - | 495 | 482,29 |
3) средняя ЗП в цехе №2:
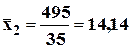д.ед.
4) групповая дисперсия в цехе №2:
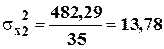
Распределение численности по уровню ЗП на предприятии
| Дневная ЗП рабочих, д.ед. | общее число рабочих, чел. (fj общ) | xj, д.ед. | xj*fj общ |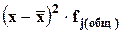 
|
| 8-10 | 8 | 9 | 72 | 288,00 |
| 10-12 | 8 | 11 | 88 | 128,00 |
| 12-14 | 11 | 13 | 143 | 44,00 |
| 14-16 | 20 | 15 | 300 | 0,00 |
| 16-18 | 13 | 17 | 221 | 52,00 |
| 18-20 | 7 | 19 | 133 | 112,00 |
| 20-22 | 8 | 21 | 168 | 288,00 |
| Итого | 75 | - | 1125 | 912,00 |
5) общая средняя ЗП:
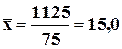д.ед.
6) общая дисперсия:
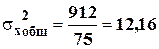
7) средняя групповых дисперсий: 
8) межгрупповая дисперсия:
.
9) Правило сложения дисперсий: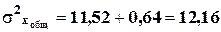 
10) Корреляционное отношение: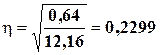 
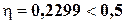– влияние факторного признака отсутствует.
