Магнитное поле тороидального и длинного соленоидов

Соленоид-это катушка, которая используется для создание магнитного поля

Пусть катушка равномерного помотана на кольцевой каркас с круговым поперечным сечением (тороид). Обозначим через 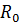средний радиус тора, через радиус поперечного сечения катушки.

Применим закон Ампера к окружности, проведенной внутри тора в плоскости, перпендикулярной оси его симметрии ОО’, с центром, лежащим на этой оси. Радиус этой окружности обозначим через r.

так как ток пересекает круг, ограниченный окружностью l, w раз, где w-число витков катушки. Вследствие симметрии системы токов, создающих магнитное поле, и самого магнитного поля его силовые линии являются окружностями. Одна из них совпадет с окружностью на которой и, кроме того, B = const:

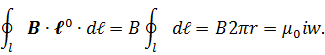
Следовательно, внутри тороида

Снаружи тороида , или 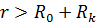, величина B сохраняет постоянный знак в следствии симметрии магнитного поля, и поэтому В =0

Теперь рассмотрим предельный случай, когда . На единицу длинны бесконечно длинной прямой катушки приходится витков.

Применим закон Ампера к прямоугольному контуру , две стороны которого параллельны оси катушки (одна расположена внутри катушки, другая снаружи) и имеют единичную длину, а две других (малой длины) перпендикулярны боковой поверхности катушки:

Снаружи катушки тороида (бесконечно большого радиуса) В =0. Внутри катушки вектор В направлен по ее оси, на поперечных сторонах контура , следовательно,