Условие соленоидальности магнитного поля

Силовые линии магнитного поля, возбужденного длинным прямолинейным проводом с током, представляют собой окружности, лежащие в плоскости, перпендикулярной проводу, с центром внутри провода (как это следует из формулы (2)). Эксперименты с магнитным полем различных устройств подтверждают предположение о замкнутости магнитных силовых линий в пространстве. Каждая силовая линия входит в объем, ограниченный замкнутой поверхностью, и выходит из него. Отсюда следует заключение о том, что магнитный поток сквозь любую замкнутую поверхность должен быть равен нулю.

    Магнитный поток сквозь поверхность S по определению равен:

Нормаль задает направления вычисления потока (направление потока).

Магнитный поток сквозь замкнутую поверхность равен нулю:

 

это условие непрерывности магнитного потока. В дифференциальной форме

                                                                                    (3)

Оно является признаком соленоидальности магнитного поля.

Закон полного тока

Магнитное поле является соленоидальным. Согласно основной теореме векторного анализа оно обладает векторным потенциалом

 

 

 

и может быть представлено в виде

 

где интегрирование выполняется по всему неограниченному трехмерному пространству. Для того чтобы последнее соотношение превратилось в физический закон, нужно экспериментально установить, как связан rot B с источниками магнитного поля (электрическими токами и намагниченными массами)

    Вновь обратимся к формуле (2), описывающей магнитное поле длинного прямолинейного провода с током

Вычислим циркуляцию магнитной индукции по окружности 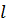радиуса r, лежащей в плоскости, перпендикулярной проводу, с центром на оси провода:

 

Циркуляция по произвольной кривой , охватывающей провод с током, также равна . Чтобы убедится в этом, разобьем контур 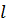на участки , каждый из которых заменим элементом окружности радиуса .Сумма интегралов по дугам окружностей дает , а сумма интегралов по радиальным отрезкам равна нулю, так как на них B 0.

Если кривая l является пространственной и каждый ее элемент разлагается на три составляющих , и  (последняя в направлении вдоль провода), то результат интегрирования не изменяется, так как на участках аксиального направления B =0.

     Формула (6) была проверена экспериментально в магнитных полях разных проводников с током и получила название закона Ампера (частный случай закона полного тока). Если сквозь поверхность S, ограниченную контуром l, проходит несколько проводников с токами, то циркуляция магнитной индукции пропорциональна алгебраической сумме токов. В системе токов, показанной на рис. 6,

(.Ток не пересекает поверхность S связано и не влияет на величину циркуляции. Направление нормали  к поверхности S связано с направлением обхода контура l правилом правого винта. Знак перед током в правой части последней формулы определяется по совпадению (плюс) или несовпадению (минус) направления тока с направлением нормали на поверхности S.

    В дифференциальной форме закон Ампера записывается в виде

Контур , ограничивающий элементарную площадку , выбранную внутри проводника с током, охватывает ток .

Система дифференциальных уравнений (3) и (7)

описывает магнитное поле, возбужденное электрическими токами (при отсутствии намагниченных тел).

Формула Био-Совара

Подставим выражения rot B из формулы (7) в формулы (4) и (6):

 

(9)

где интегрирование выполняется по объему, занятому проводниками с током (вне проводников ). Формула (9) была предложена Лапласом на основании опытов, выполненных Био и Саваром и получила название закона Био – Савара. Она используется для расчета магнитных полей систем проводников, в которых известно распределение тока, т.е. функция известна .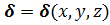

Если ток протекает по тонким проводам и магнитное поле определяется на достаточно большом удалении от провода, то , где  - единичный вектор касательной к линии провода l с током i. В этом случае формулы (8) и (9) можно представить в следующем виде

    Формулы (8) и (9) можно использовать для расчета магнитных полей внутри проводников, по которым текут электрические токи. Формулы (10) и (11) применяются для расчета полей на достаточно большом рассоянии от проводников. В точках контура l векторный потенциал А и магнитная индукция В обращаются в бесконечность. Во всех формулах, записанных выше, предполагается пока, что магнитное поле создается постоянными токами и не изменяется с течением времени.