2020-04-07
209
Стационарное магнитное поле можно описать с помощью векторного потенциала A, который сводится уравнениями:
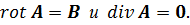
Стационарное электрическое поле можно описать скалярным электрическим потенциалом, который вводится условием:
Закон электромагнитной индукции связывает переменные электрические и магнитные поля, через потенциалы A и φ он представляется в виде:
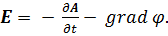(11)
Первое слагаемое задает вихревую (индуцированную, соленоидальную) составляющую электрического поля, второе – безвихревую (потенциальную) составляющую, которая создается электрическими зарядами.
Выведем уравнения, которым подчиняются электродинамические потенциалы A и φ.
Продифференцируем уравнение 
и учтем закон полного тока в форме Ампера:
Пологая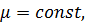 
преобразуем вторую производную векторного потенциала по известному правилу векторного анализа, а так же учтем, что
где E представляется по формуле (11):
Так как 
то
(12)
|
|
|
Итак, векторный потенциал удовлетворяет неоднородному уравнению теплопроводности.
Остается получить уравнение для электрического потенциала. В постулат Максвелла
Подставим выражение (11) для напряженности электрического поля:
Так как 
то
(13)
Скалярный (электрический) потенциал удовлетворяет уравнению Пуассона. Уравнения (11) и (12) образуют систему уравнений для электродинамических потенциалов квазистационарного электромагнитного поля.
Допустим для простоты, что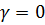 
и электромагнитное поле удовлетворяет уравнениям
Перемещение зарядов в пространстве вызывает мгновенное изменение электрического и магнитного полей. Такое электромагнитное поле, которое изменяется синхронно со своими источниками, называется квазистационарным. Опыт показывает, что возмущения в электромагнитном поле распространяются с большой, но конечной (близкой к скорости света) скоростью. Значит, уравнения квазистационарного поля дают приближенную картину электродинамических процессов. В электротехнике обычно применяются теория электромагнитного поля в квазистационарном приближении.
