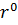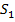2020-04-07
852
Логарифмический потенциал
Электрическое поле равномерно заряженной прямой
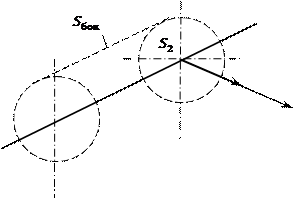
Пусть бесконечно длинная нить равномерно заряжена с линейной плотностью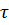 
. Электрическое поле одинаково во всех плоскостях, перпендикулярных нити, и обладает осевой симметрией. Совместим ось цилиндрической системы координат с заряженной нитью (рис. 15), тогда
 |
|
|
|
|
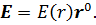
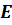
Δl
Рис. 15. Заряженная нить и воображаемая цилиндрическая поверхность
Выделим участок заряженной нити длиной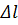 
и построим вокруг него круговой цилиндр так, чтобы его ось совпала с нитью. Применим к поверхности цилиндра 
электростатическую теорему Гаусса:
|
|
|
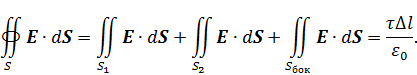
На торцах цилиндра векторы напряженности и нормали перпендикулярны, потоки электрического поля сквозь поверхности 
и 
равны нулю. Следовательно,
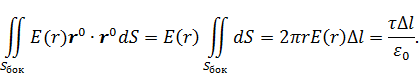
В итоге
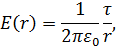
где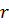 
– расстояние от заряженной оси до точки поля. Выберем точку нулевого потенциала на расстоянии r0 от оси; потенциал электрического поля равен
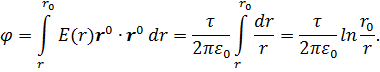
Если точку нулевого потенциала не фиксировать, то
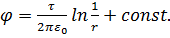(16)
Поле равномерно заряженного кругового цилиндра
Пусть ось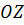 
цилиндрической системы координат совпадает с осью бесконечно длинного цилиндра радиуса r0, заряженного с объемной плотностью ρ. Электрическое поле обладает осевой симметрией 
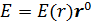(рис. 16).
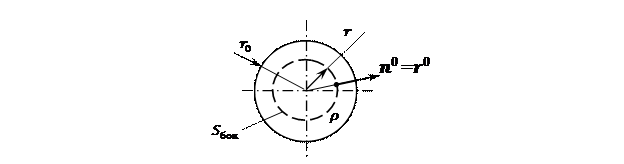
Рис. 16. Поперечное сечение заряженного цилиндра и воображаемой цилиндрической поверхности
Построим воображаемый цилиндр длиной 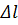вдоль оси 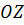радиусом 
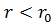. Применим к его поверхности 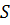электростатическую теорему Гаусса. Поток электрического поля сквозь основания этого цилиндра равен нулю. Внутри него содержится заряд 
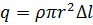. Следовательно,
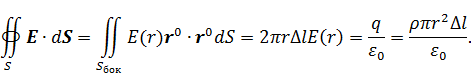
Таким образом,
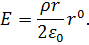
На оси заряженного цилиндра E=0; на его поверхности
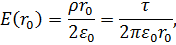
где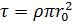 
– заряд, приходящийся на единицу длины заряженного цилиндра.
Чтобы определить напряженность электрического поля вне заряженного цилиндра, нужно применить теорему Гаусса к воображаемой цилиндрической поверхности радиуса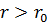 
и длинной .
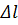В этом случае
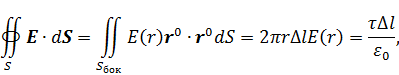
следовательно,
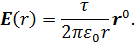
Вне заряженного цилиндра электрическое поле такое же, как поле заряженной нити.
