Система двух проводников

    Пусть два проводника расположены вблизи друг от друга (рис 19). Если первому проводнику сообщить заряд q₁ (q₂=0), то оба проводника приобретут потенциалы  и , где α₁₁ и α₁₂ – потенциальные коэффициенты. Если второму проводнику сообщить заряд q₂, оставив первый проводник нейтральным (q ₁ =0), то  и . Если заряжены оба проводника, то согласно принципу наложения

, .

        

 

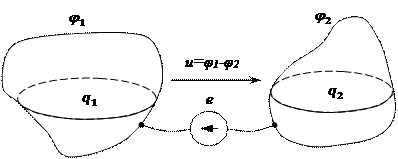
Рис.19. Система двух заряженных проводников

 

Если проводники заряжены от источника ЭДС, как показано на рис.19, то 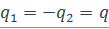. Зависимости между потенциалами и зарядами принимают вид , . Напряжение между проводниками пропорционально заряду q:

Коэффициент пропорциональности C называется электрической емкостью между проводниками, .

     Два проводника, изолированных друг от друга, образуют электрический конденсатор. В электрических цепях конденсаторы работают в таких условиях, что заряды проводников равны по величине и противоположны по знаку. Поэтому потенциальные коэффициенты проводников не представляют интереса, конденсатор характеризуется одним параметром – электрической емкостью.

    Пример. Емкость коаксиального кабеля

       Коаксиальный кабель – это два длинных металлических провода, разделенных слоем изоляции, один из которых (цилиндрический) находится внутри другого (трубчатого). Первый провод имеет круговое поперечное сечение, второй – кольцевое сечение, оси симметрии проводов совпадают (рис 20).

 

 

 

 

Рис.20. Поперечное сечение коаксиального кабеля

 

       Пусть заряд внутреннего провода равен q, на единицу длины кабеля приходится заряд , где L – длина кабеля. Заряд наружного провода равен (-q). Электрическое поле внутри кабеля является плоскопараллельным и обладает цилиндрической симметрией.

    Построим воображаемую цилиндрическую поверхность радиуса r ₁< r<r _2, ось которой совпадает с осью кабеля. Длину соответствующего ей цилиндра положим равной единице. Применим к поверхности цилиндра S электростатическую теорему Гаусса. Электрический поток сквозь основание цилиндра равен нулю, на боковой поверхности цилиндра вектор напряженности  направлен в радиальном направлении, поэтому

 

Напряженность электрического поля в изоляции между проводами

 

 

 Напряжение между проводами

 

 Электрическая емкость кабеля

 

 

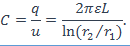
 Чем тоньше изоляция кабеля, тем ближе к 1 отношение , тем меньше   тем больше емкость кабеля.

      Вне кабеля электрического поля нет, потому что электрический поток сквозь любую цилиндрическую поверхность радиуса 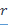, большего, чем 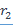, равен нулю (ибо внутри этой поверхности сумма положительных и отрицательных зарядов равна нулю).

 

 

Краткое содержание пятой лекции. Двумерные электрические поля  описывается логарифмическим потенциалом

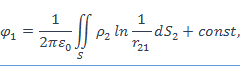
где S – поперечное сечение области, содержащей распределенный заряд, плоскостью XOY; 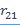 – расстояние между точками 2 и 1 в этой плоскости.

В состоянии, когда все заряды неподвижны электрическое поле внутри проводника отсутствует. Поверхность проводника является эквипотенциальной (т.е. поверхностью равного потенциала). Напряженность электрического поля на этой поверхности имеет только нормальную составляющую

где  - нормаль, внешняя по отношению к проводнику. Способность проводника накапливать электрический заряд характеризуется его емкостью

(точка нулевого потенциала на бесконечности).

Два проводника образуют конденсатор в условиях, когда их заряды равны по величине и противоположны по знаку. Способность конденсатора накапливать заряды характеризуется его емкостью

где q – заряд положительного проводника, u – напряжение, направленное от положительного к отрицательному проводнику ().

 

Дополнение к §10. Проводник во внешнем электрическом поле

Пусть, для определенности, проводник находится в поле точечного заряда (рис. 18). Потенциал проводника равен

Здесть точка 1 находится на поверхности проводника S, σ – плотность заряда на поверхности проводника, точечный заряд q ₃ – помещен в точке 3. Заряд проводника может быть любым, в частности, может быть равен нулю.

      Если точечного заряда нет (), а проводник заряжен, то его потенциал пропорционален заряду: , где  - собственный потенциальный коэффициент проводника. Если проводник не заряжен (), то в поле точечного заряда  он приобретает потенциал , где  - взаимный потенциальный коэффициент проводника и предельно малого тела, несущего заряд . Согласно принципу наложения .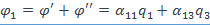

 

Составляющая потенциала

где  - плотность заряда на поверхности проводника в случае, когда он не заряжен ); индексы точек источника и наблюдения опущены для сокращения записи. Другая составляющая потенциала

 

где  - плотность заряда на поверхности проводника, когда он заряжен 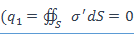), а . Распределение зарядов на поверхности проводника 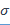 в общем случае складывается из распределений  и , т.е. . Теперь выражение для потенциала проводника можно представить в виде

        Очевидно, что эта формула эквивалентна первоначальному представлению потенциала. Она может быть полезной при расчете электрического поля заряженного проводника в присутствии точечного заряда, в частности, для определения потенциальных коэффициентов.