Пусть точка  под действием силы
под действием силы 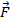 перемещается вдоль непрерывной плоской кривой
перемещается вдоль непрерывной плоской кривой 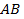 в направлении от точки
в направлении от точки 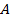 к точке
к точке 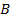 . Если
. Если 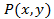 и
и 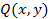 координаты силы
координаты силы 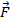 в каждой точке
в каждой точке 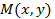 кривой
кривой 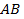 , то работа силы
, то работа силы 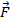 при перемещении точки
при перемещении точки 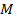 по кривой
по кривой 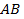 по направлению от
по направлению от 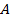 к
к 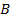 .
.
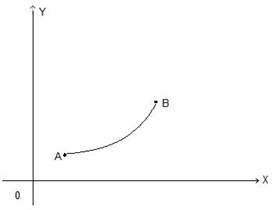
(рис. 3.3)
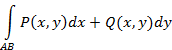
4. Условия независимости криволинейного интеграла второго рода от пути интегрирования
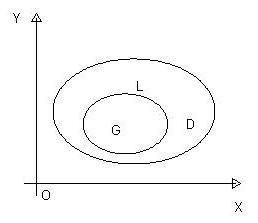
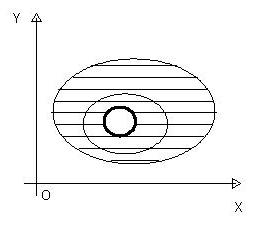
Определение 5.3 Область 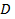 плоскости
плоскости 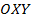 называется односвязной, если для любой замкнутой кривой
называется односвязной, если для любой замкнутой кривой 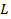 , принадлежащей области
, принадлежащей области 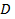 , область
, область 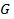 , ограниченная кривой
, ограниченная кривой 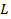 , целиком лежит в области
, целиком лежит в области 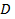 .
.
(рис. 3.4) (рис. 3.5)
Иначе говоря, односвязность области означает отсутствие «дыр».
Теорема 5.2.
Пусть функции 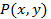 и
и 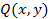 определены и непрерывны вместе со своими частными производными
определены и непрерывны вместе со своими частными производными 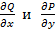 в некоторой замкнутой односвязной области
в некоторой замкнутой односвязной области 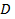 . Тогда следующие четыре условия эквивалентны:
. Тогда следующие четыре условия эквивалентны:
1.)Для любой замкнутой кусочно-гладкой кривой 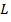 , расположенной в области
, расположенной в области 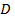 ,
,
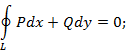
2.)Для любых двух точек 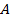 и
и 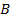 области
области 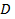 значение интеграла
значение интеграла
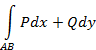
не зависит от выбора пути интегрирования, целиком лежащего в 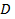 ;
;
3.)Выражение 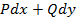 представляет собой полный дифференциал некоторой функции, т.е. существует такая функция
представляет собой полный дифференциал некоторой функции, т.е. существует такая функция 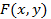 , определенная в
, определенная в 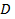 , что
, что
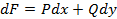 .
.
4.)В области D всюду справедливо равенство:
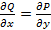 (1)
(1)
Эквивалентность приведенных четырех условий означает, что из справедливости любого одного условия следует справедливость остальных.
Для доказательства теоремы 5.2. воспользуемся следующей схемой: 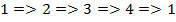 .
.
Первый этап:1=>2. Пусть произвольные точки области 
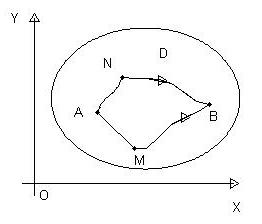
(рис. 3.6)
Из точки 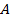 в
в 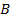 можно прийти по разным кривым, соединяющим эти две точки и целиком лежащим в области
можно прийти по разным кривым, соединяющим эти две точки и целиком лежащим в области 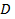 . Пусть
. Пусть 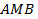 и
и 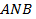 две кусочно-гладкие кривые, соединяющие точки
две кусочно-гладкие кривые, соединяющие точки 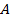 и
и 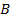 . Тогда кривая
. Тогда кривая 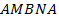 кусочно-гладкая, замкнутая кривая, целиком лежащая в области
кусочно-гладкая, замкнутая кривая, целиком лежащая в области 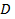 . Cогласно условию 1:
. Cогласно условию 1:
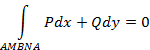
С другой стороны,
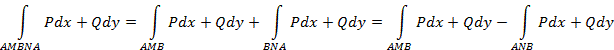
Следовательно,
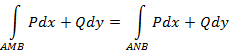
т.е. условие 2.) выполняется.
Второй этап: 2=>3. Пусть интеграл 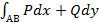 не зависит от выбора пути интегрирования, а зависит только от точек
не зависит от выбора пути интегрирования, а зависит только от точек 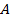 и
и 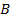 .
.
Фиксируем точку 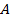 =
= 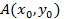 области
области 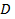 .
.
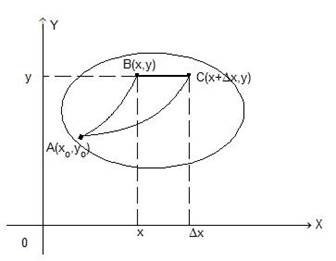
(рис. 3.7)
Тогда интеграл будет некоторой функцией координат 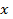 и
и 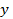 точки
точки 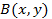
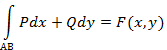
Покажем, что функция 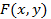 дифференцируема и что
дифференцируема и что
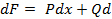 (2)
(2)
Для этого достаточно доказать, что в каждой точке 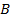 области
области 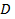 существуют частные производные
существуют частные производные 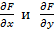 , причем
, причем
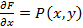 ,
, 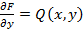 (3)
(3)
Так как 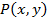 и
и 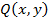 непрерывны в
непрерывны в 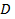 , то из (3) следует дифференцируемость функции
, то из (3) следует дифференцируемость функции 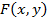 и равенство (2).
и равенство (2).
Рассмотрим приращение функции 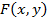 в точке
в точке 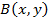 .Пусть
.Пусть 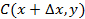 - точка области
- точка области 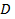 .
.
Тогда:
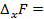
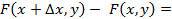
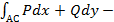
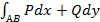 =
= 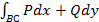 .
.
Так как по условию интеграл не зависит от кривой интегрирования, то возьмем путь от 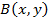 до
до 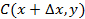 прямолинейным, тогда
прямолинейным, тогда
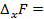
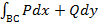 =
= 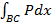 =
= 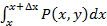
Применим теорему о среднем и получим:
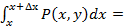
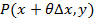 , где
, где 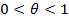 .
.
Откуда:
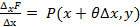 ,, где
,, где 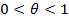 .
.
Следовательно:
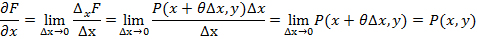
Итак, 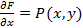 .
.
Аналогично доказывается, что 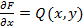 . Тогда
. Тогда
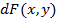 =
= 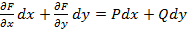 . Таким образом, выражение
. Таким образом, выражение 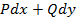 представляет полный дифференциал функции
представляет полный дифференциал функции 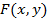 .
.
Докажем теперь, что 3=>4.
Итак, пусть в области 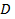 определена некоторая дифференцируемая функция
определена некоторая дифференцируемая функция 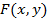 такая, что
такая, что 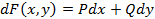 . Тогда
. Тогда 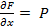 ,
, 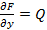 . Тогда из теоремы о равенстве смешанных производных следует, что
. Тогда из теоремы о равенстве смешанных производных следует, что 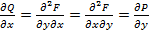 . Т.е.
. Т.е. 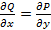 .
.
Нам остается доказать, что 4=>1.
Итак пусть 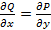 . Докажем, что
. Докажем, что 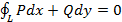 для любой кусочно-гладкой кривой, лежащей в области
для любой кусочно-гладкой кривой, лежащей в области 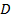 . Обозначим через
. Обозначим через 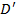 область, ограниченную кривой L (здесь используется односвязность области
область, ограниченную кривой L (здесь используется односвязность области 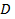 )
)
Пользуясь формулой Грина, получим
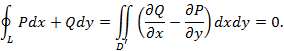
Тем самым, теорема 5.2. доказана.
Замечание: Условия непрерывности функции 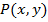 ,
, 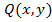 и их частных производных
и их частных производных 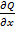 ,
, 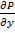 являются существенными.
являются существенными.
Пример. Рассмотрим интеграл
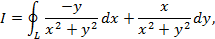
где 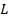 – окружность радиуса
– окружность радиуса 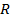 с центром в начале координат.
с центром в начале координат.
Здесь 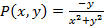 ,
, 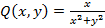 .
.
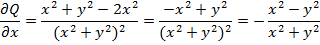
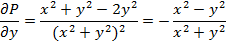
Видим, что условие независимости интеграла от выбора пути формально выполнено, но, однако, интеграл по окружности L нулю не равен. Действительно, зададим уравнение окружности: 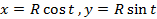 ,
, 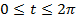
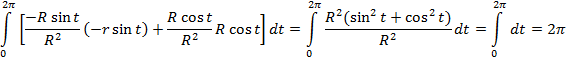
Никакого противоречия тут нет. Просто не выполнено одно из условий теоремы: функции 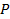 и
и 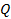 , и их частные производные
, и их частные производные 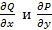 , не определены в точке (0, 0), а круг, ограниченный окружностью
, не определены в точке (0, 0), а круг, ограниченный окружностью 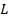 , с выброшенной точкой
, с выброшенной точкой  уже не является связной областью.
уже не является связной областью.
5. Потенциал векторного поля. Вычисление криволинейного интеграла с помощью потенциала.
Вернемся к теореме 5.2. Было доказано, что если функции 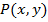 и
и 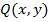 и их частные производные
и их частные производные 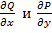 непрерывны в замкнутой области
непрерывны в замкнутой области 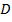 , то выражение
, то выражение 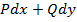 является полным дифференциалом некоторой функции в области
является полным дифференциалом некоторой функции в области 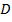 тогда и только тогда, когда
тогда и только тогда, когда
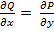 (4)
(4)
Было также доказано, что если равенство (4) выполнено, то условию
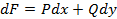 удовлетворяет функция
удовлетворяет функция
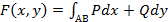 (5)
(5)
где 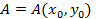 ,
, 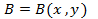 . При выполнении равенства (4) интеграл в правой части равенства (5) не зависит от пути интегрирования
. При выполнении равенства (4) интеграл в правой части равенства (5) не зависит от пути интегрирования 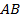 , а зависит лишь от точек
, а зависит лишь от точек 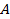 и
и 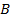 . Поэтому этот интеграл принято обозначать следующим образом
. Поэтому этот интеграл принято обозначать следующим образом
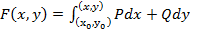 (6)
(6)
Определение 5.4. Дифференцируемую в области 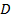 функцию
функцию 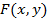 будем называть потенциалом поля
будем называть потенциалом поля 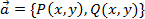 и
и
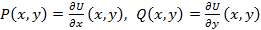 (7)
(7)
Поле 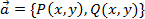 , при этом, будем называть потенциальным.
, при этом, будем называть потенциальным.
Пусть 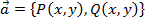 потенциальное поле, т.е. выполняются равенства (7), тогда
потенциальное поле, т.е. выполняются равенства (7), тогда 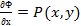 и
и 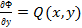 .
.
Рассмотрим функцию 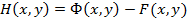 и вычислим частные производные
и вычислим частные производные 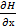 и
и 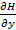 .
.
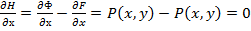 ,
, 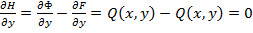 .
.
Следовательно, 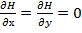 из чего следует, что
из чего следует, что 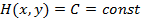 , т.е.
, т.е.
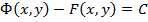 или
или 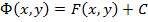 .
.
Взяв в последнем равенстве 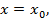
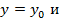 , учитывая
, учитывая 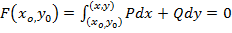 , получим
, получим 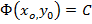 , т.е.
, т.е.
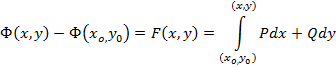
Если в этом равенстве положим 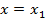 ,
, 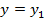 , то получим
, то получим
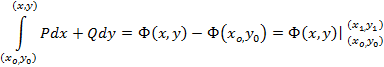
Полученная формула аналогична формуле Ньютона-Лейбница, но справедлива только при условии независимости криволинейного интеграла от выбора пути интегрирования.
Исходя из приведённых рассуждений, теперь можно показать способ восстановления 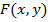 , полный дифференциал которого есть выражение
, полный дифференциал которого есть выражение 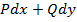 .
.
Формула
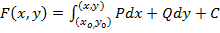 (8)
(8)
где 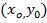 фиксированная точка, а
фиксированная точка, а 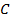 – произвольная постоянная, и даёт возможность определить все функции, имеющие подынтегральное выражение своим полным дифференциалом.
– произвольная постоянная, и даёт возможность определить все функции, имеющие подынтегральное выражение своим полным дифференциалом.
Для отыскания 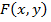 по формуле (8) достаточно, выбрав любую точку
по формуле (8) достаточно, выбрав любую точку 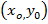 в области D, вычислить криволинейный интеграл по любой кривой, соединяющей точки
в области D, вычислить криволинейный интеграл по любой кривой, соединяющей точки 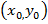 и
и 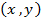 . Так как в формуле (8) интеграл не зависит от выбора пути, то удобно, например, за путь интегрирования брать ломанную, звенья которой параллельны осям координат. Тогда
. Так как в формуле (8) интеграл не зависит от выбора пути, то удобно, например, за путь интегрирования брать ломанную, звенья которой параллельны осям координат. Тогда
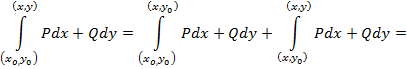
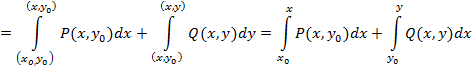
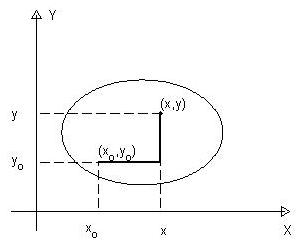
(рис. 3.8)
формула (8) принимает вид
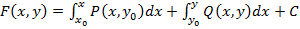 ,
,
Где первый определенный интеграл вычисляется при постоянном 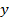 , равном
, равном  , а второй – при постоянном
, а второй – при постоянном 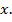
 2020-04-12
2020-04-12 703
703