Повторные операции векторного поля

                                        (7)

Оператор  называется оператором Лапласа.

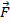Рассмотрим ). Будем предполагать, что координаты  векторной функции  непрерывны вместе со своими частными производными второго порядка включительно. Тогда

 ( =

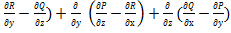Так как , в силу непрерывности этих частных производных второго порядка. Таким образом

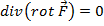                                            (8)

Можно привести очень простое, формальное доказательство равенства (5) с привлечением оператора Гамильтона.

Рассмотрим теперь , где  скалярная функция непрерывная вместе со своими частными второго порядка.

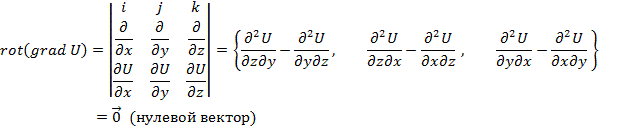
Этот же результат легко получить с помощью оператора :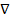

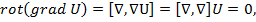
так как векторное произведение одинаковых векторов равно нулю.