Скалярное поле. Пусть в области 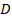 пространства
пространства  определена функция
определена функция  ,
,  . Тогда будем говорить, что в области
. Тогда будем говорить, что в области 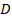 задано скалярное поле. Таким образом, скалярное поле задается с помощью функции
задано скалярное поле. Таким образом, скалярное поле задается с помощью функции  , которая называется скалярное функцией.
, которая называется скалярное функцией.
Примером скалярное поля может служить поле температуры воздуха в некотором помещении, если температуру рассматривать как функцию точки. В точках, расположенных ближе к источнику теплоты, температура выше, дальше от источника теплоты – ниже. Если окажется, что температура везде одинаковая, то в этом случае скалярное поле постоянно.
Векторное поле. Пусть в области 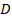 пространства
пространства  заданы функции
заданы функции  ,
,  (
( ,
,  ,
,  ) где
) где  , и определён вектор
, и определён вектор 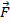 с координатами {
с координатами {  ,
,  } ({
} ({  ,
,  ,
,  }). Тогда
}). Тогда  {
{  ,
,  } (
} ( {
{  ,
,  ,
,  }) задает в области
}) задает в области 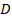 векторное поле и называется векторной функцией.
векторное поле и называется векторной функцией.
Потенциальное поле. Рассмотрим некоторое скалярное поле  в области
в области 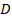 . Если в каждой точке
. Если в каждой точке  из
из 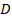 определен вектор
определен вектор  , то поле этого вектора называется потенциальным полем. Само скалярное поле называется при этом потенциалом векторного поля, а вектор, определяющий потенциальное поле, часто называют потенциальным вектором, т.е. вектор
, то поле этого вектора называется потенциальным полем. Само скалярное поле называется при этом потенциалом векторного поля, а вектор, определяющий потенциальное поле, часто называют потенциальным вектором, т.е. вектор  (
( ) потенциальный, если найдется такая скалярная функция
) потенциальный, если найдется такая скалярная функция  , что
, что
 =
= 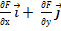 (
( =
=  ) (1)
) (1)
Возникает вопрос, при каких условиях данное векторное поле  (M) потенциальное.
(M) потенциальное.
Пусть в области 
 и
и  - проекции вектора
- проекции вектора 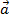 на оси координат
на оси координат  ,
,  соответственно, т.е.
соответственно, т.е.

В силу соотношения (1) векторное поле  является потенциальным, если найдётся функция
является потенциальным, если найдётся функция 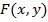 такая, что
такая, что
 (2)
(2)
В этом случае 
В теореме 5.2 (о независимости криволинейного интеграла от пути интегрирования) было показано, что выражение  (где
(где  ,
,  непрерывные функции, имеющие непрерывные частные производные первого порядка) полный дифференциал некоторой функции
непрерывные функции, имеющие непрерывные частные производные первого порядка) полный дифференциал некоторой функции 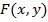 тогда и только тогда, когда
тогда и только тогда, когда  и
и  удовлетворяют условиям
удовлетворяют условиям
 (3)
(3)
Но если  , то справедливы и равенства (2), т.е. условие (3) как раз и означает, что данное векторное поле потенциальное. Функция
, то справедливы и равенства (2), т.е. условие (3) как раз и означает, что данное векторное поле потенциальное. Функция 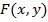 в этом случае называется потенциальной функцией поля.
в этом случае называется потенциальной функцией поля.
Градиент скалярного поля. Пусть в области 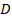 в пространстве
в пространстве  определена некоторая функция
определена некоторая функция  . Градиентом скалярного поля
. Градиентом скалярного поля  называется вектор
называется вектор  составим формальный вектор
составим формальный вектор  . Определим произведение формального вектора
. Определим произведение формального вектора  на скалярную функцию
на скалярную функцию  – равенством
– равенством 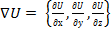 . Таким образом,
. Таким образом, 
Дивергенция векторного поля. Пусть в области 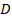 задано векторное поле
задано векторное поле  {
{  ,
,  ,
,  }. Функции
}. Функции  ,
,  ,
,  непрерывны вместе с частными производными. Дивергенцией векторного поля
непрерывны вместе с частными производными. Дивергенцией векторного поля 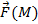 называется функция div
называется функция div 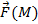 , определяемая равенством
, определяемая равенством
div 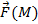 =
=  (4)
(4)
Ротором векторного поля 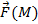 называется вектор rot
называется вектор rot 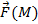 , определяемый равенством
, определяемый равенством
rot 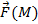 ={(
={( (5)
(5)
Пользуясь оператором Гамильтона 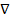 , rot
, rot 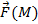 можно записать в виде
можно записать в виде
rot 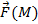 =
=  или rot
или rot  (6)
(6)
 2020-04-12
2020-04-12 306
306








