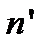 , находящуюся в среде с показателем преломления
, находящуюся в среде с показателем преломления 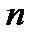 . Пусть на нее под углом
. Пусть на нее под углом 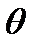 падает плоская волна монохроматического света. В результате многократных отражений образуются плоские волны
падает плоская волна монохроматического света. В результате многократных отражений образуются плоские волны  ,
, 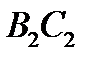 , … и
, … и 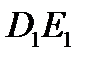 ,
, 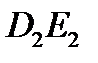 , …, отраженные и прошедшие (рис.8.29).
, …, отраженные и прошедшие (рис.8.29).
Пусть, как и раньше (глава 3), амплитуда падающей волны 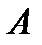 , и будем считать ее поляризованной, либо параллельно, либо перпендикулярно плоскости падения. Как и раньше, будем считать амплитуду
, и будем считать ее поляризованной, либо параллельно, либо перпендикулярно плоскости падения. Как и раньше, будем считать амплитуду  комплексной величиной, фаза которой равна постоянной части фазы соответствующей волновой функции, т.е.
комплексной величиной, фаза которой равна постоянной части фазы соответствующей волновой функции, т.е.
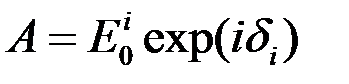
Здесь 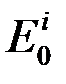 – амплитуда электрического вектора.
– амплитуда электрического вектора.
Уравнение плоской гармонической волны частотой  , идущей в направлении единичного вектора
, идущей в направлении единичного вектора 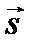 со скоростью
со скоростью 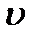 имеет известный вид (см. главу 3):
имеет известный вид (см. главу 3):
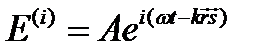 ,
,
гле 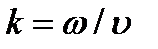 - волновое число.
- волновое число.
Из предыдущего раздела известно, что каждая из плоских волн (отраженных или прошедших) имеет постоянный фазовый сдвиг
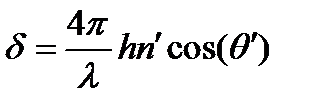
относительно предыдущей.
Обозначим френелевские амплитудные коэффициенты пропускания из воздуха в среду 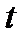 , а из среды в воздух –
, а из среды в воздух – 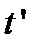 , и соответствующие коэффициенты отражения –
, и соответствующие коэффициенты отражения – 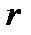 и
и 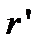 . Тогда, считая начальные фазы первых отраженных и прошедших волн
. Тогда, считая начальные фазы первых отраженных и прошедших волн 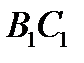 и
и 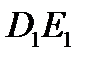 нулевыми, для комплексных амплитуд отраженных и прошедших волн получаем:
нулевыми, для комплексных амплитуд отраженных и прошедших волн получаем:
Отраженные волны:
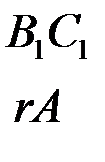 ,
, 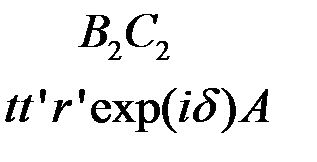 ,
, 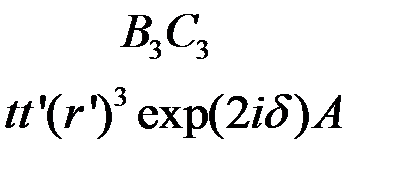 , …
, … 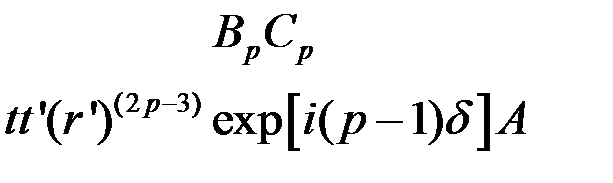 .
.
Прошедшие волны:
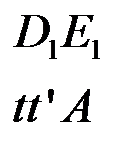 ,
, 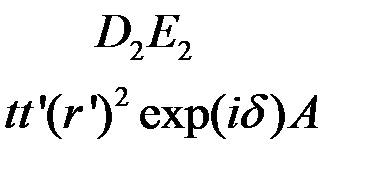 ,
, 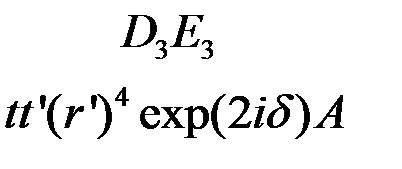 ,….
,…. 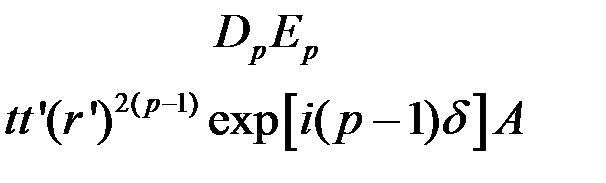
Важно обратить внимание на то, что для каждой из компонент, параллельной и перпендикулярной, справедливы соотношения:
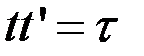 ;
; 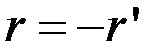 и
и 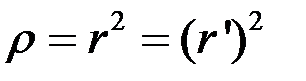 , и кроме того
, и кроме того 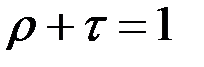 .
.
Здесь 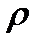 и
и  – энергетические коэффициенты пропускания и отражения.
– энергетические коэффициенты пропускания и отражения.
При суперпозиции первых p отраженных волн возникает плоская волна, амплитуда электрического вектора которой равна:
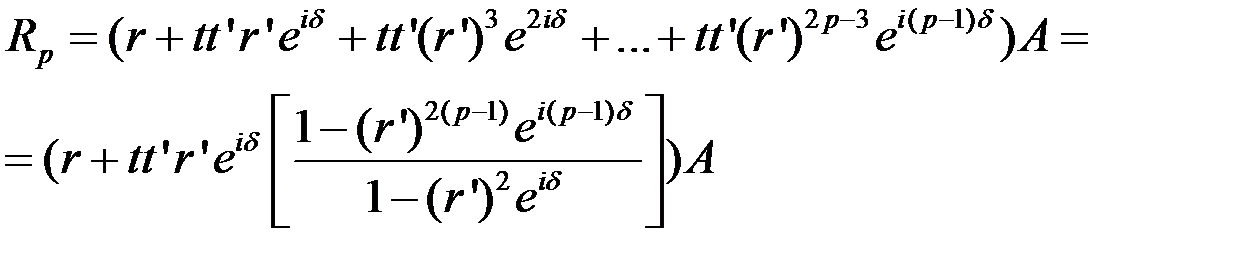
Если 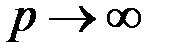 , получаем:
, получаем:
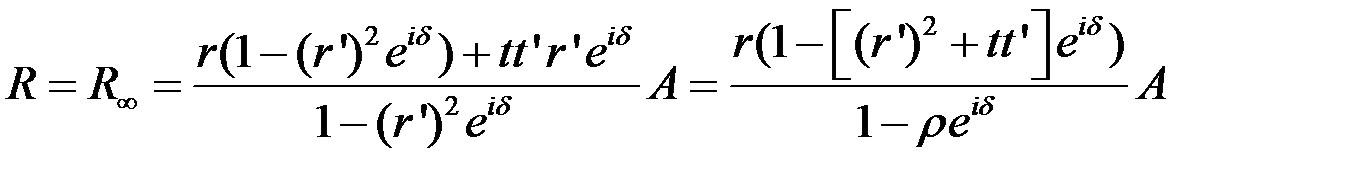
Таким образом
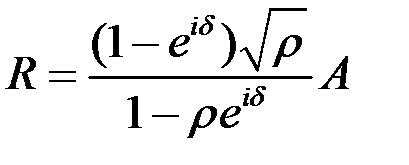 . (8.80)
. (8.80)
Интенсивность отраженного света 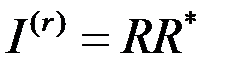 .
.
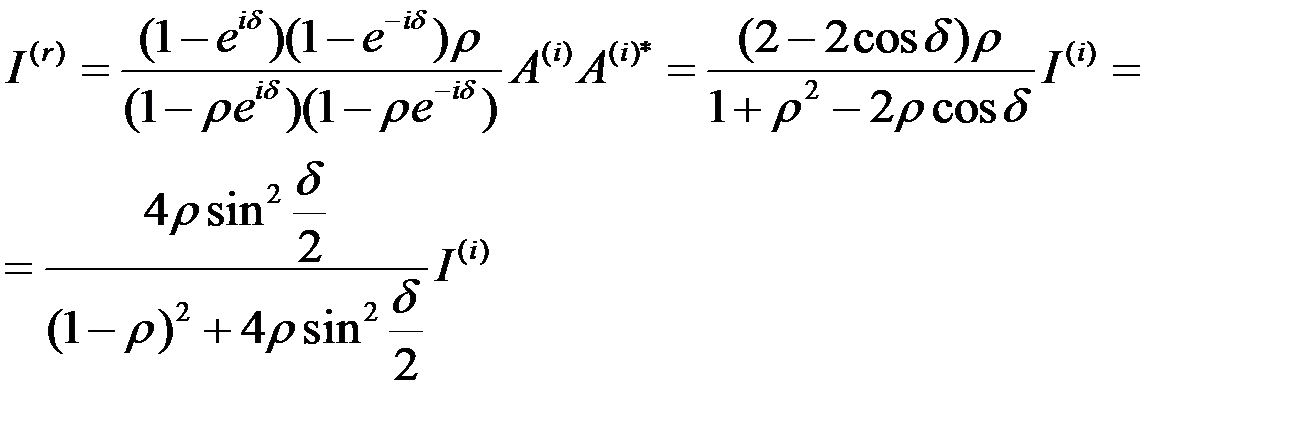 (8.81)
(8.81)
Аналогично получим выражение для интенсивности прошедшего света, а именно:
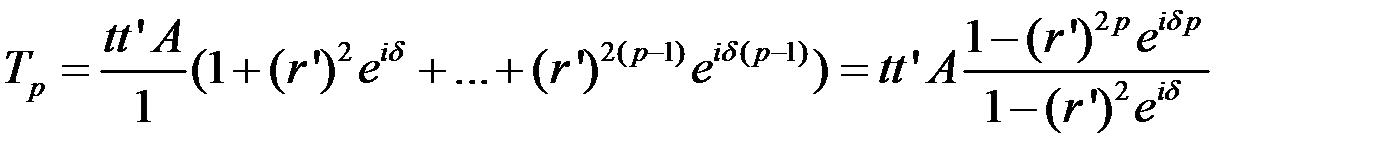
При 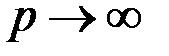 получаем:
получаем:
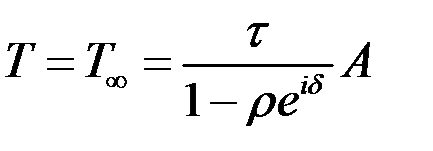 (8.82)
(8.82)
И, следовательно, интенсивность прошедшего света 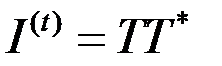
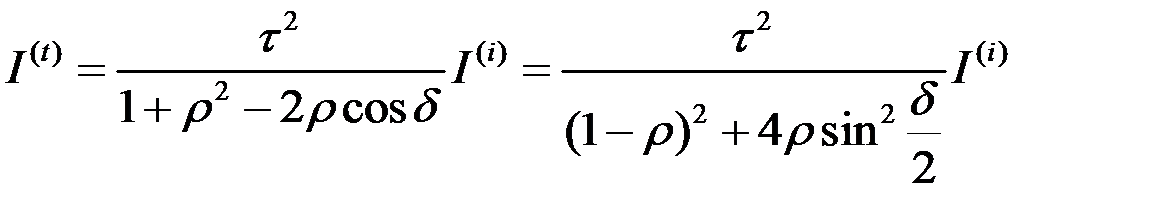 (8.83)
(8.83)
Предположим теперь, что параллельные пучки отраженного и прошедшего излучения собираются в фокальных плоскостях линз Л1 и Л2 (рис. 8.30).
Видно, что в точках P будут наблюдаться максимумы интенсивности прошедшего света, когда δ=2πm, m=1, 2, 3.., и минимумы при m=1/2, 3/2, 5/2..
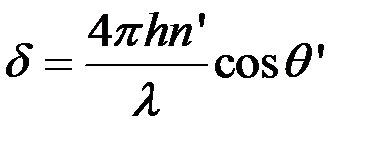 , то в фокальной плоскости линзы Л1 будут наблюдаться полосы равного наклона, соответствующие местам с постоянным
, то в фокальной плоскости линзы Л1 будут наблюдаться полосы равного наклона, соответствующие местам с постоянным 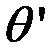 (и, следовательно,
(и, следовательно, 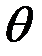 ). Аналогично в фокальной плоскости линзы Л2также будут наблюдаться полосы равного наклона, причем максимумы будут при условии δ=2πm (m=1/2, 3/2, 5/2..), а минимумы при m=1, 2, 3..
). Аналогично в фокальной плоскости линзы Л2также будут наблюдаться полосы равного наклона, причем максимумы будут при условии δ=2πm (m=1/2, 3/2, 5/2..), а минимумы при m=1, 2, 3..
Таким образом, положение максимумов и минимумов при многолучевой интерференции оказалось таким же, как и при двулучевой. В чем же особенность? Разберемся в этом подробнее.
Введем параметр:
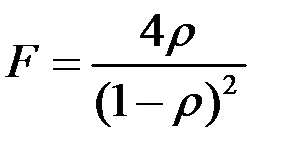 (8.84)
(8.84)
Тогда очевидно:
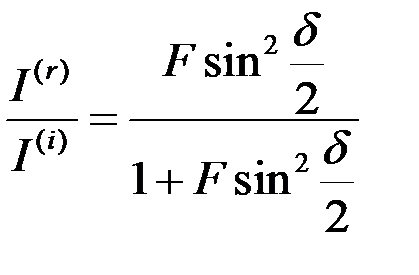 ,
, 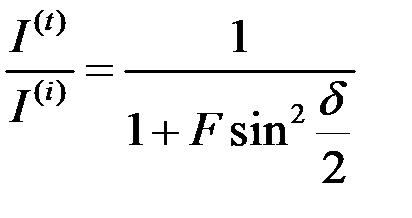 (8.25)
(8.25)
Обе картины энергетически дополнительны, в том смысле, что:
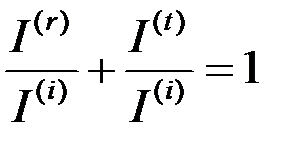 . (8.86)
. (8.86)
Когда ρмало по сравнению с единицей, F также мало и мы можем разложить в ряд выражение 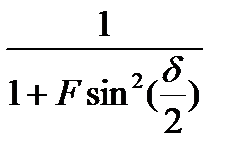 . Тогда, ограничиваясь членами с F в первой степени, получаем:
. Тогда, ограничиваясь членами с F в первой степени, получаем:
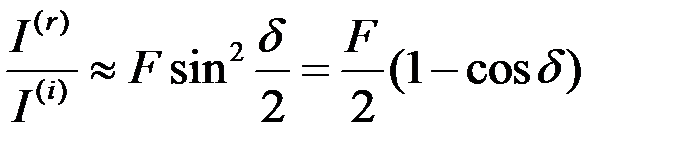 ;
; 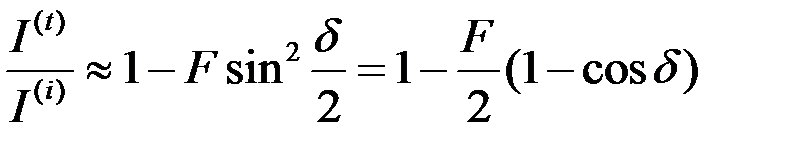 , (8.26)
, (8.26)
т.е. соотношения для интенсивности имеют вид, характерный для двулучевой интерференции.
Если ρ увеличивается (F велико), максимумы становятся значительно резче; интерференционная картина в прошедшем свете имеет вид узких светлых полос на темном фоне (в отраженном – наоборот). Резкость полос обычно оценивают полушириной интенсивности, точнее говоря, относительной полушириной. Резкостью 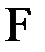 будем называть отношение расстояния между полосами к ширине. Удобно выразить эти величины в долях δ. Тогда
будем называть отношение расстояния между полосами к ширине. Удобно выразить эти величины в долях δ. Тогда
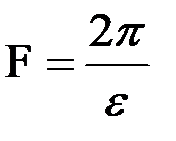 , (8.27)
, (8.27)
где ε – полуширина максимума интенсивности, причем (см. рис. 8.31)
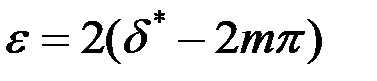 .
.
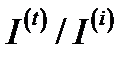 от от 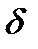 при различных значениях параметра при различных значениях параметра 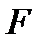
|
Для нахождения ε положим в (8.26) 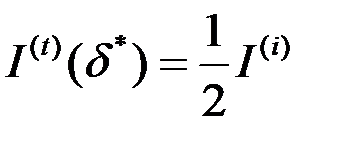 , и тогда
, и тогда
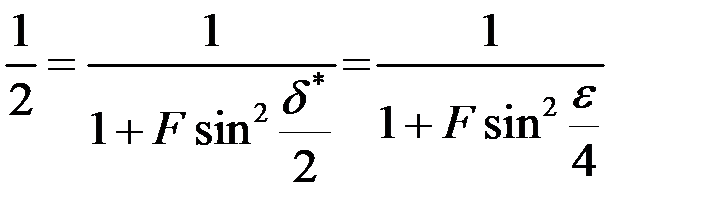 .
.
Отсюда следует, что
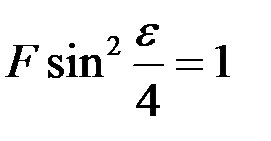 (8.28)
(8.28)
При больших F значение ε становится настолько малым, что можно считать 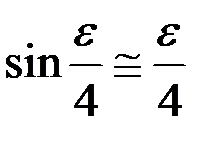 , и тогда из (8.28)
, и тогда из (8.28)
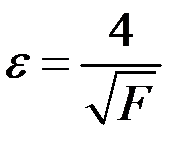 .
.
Следовательно, резкость 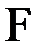 равна (из (8.27))
равна (из (8.27))
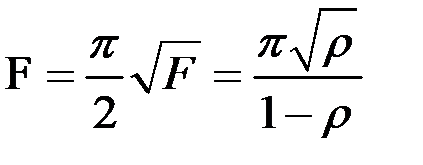 .
.
До сих пор мы предполагали, что свет строго монохроматичен. В случае квазимонохроматического света распределение интенсивности равно сумме распределений интенсивностей типа (8.25), обусловленных каждой монохроматической компонентой λ0. Если эти компоненты занимают область длин волн Δλ0 вблизи средней длины волны 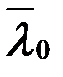 , то максимумы порядка m распределены в области, соответствующей Δδ в картине, получающейся на длине волны
, то максимумы порядка m распределены в области, соответствующей Δδ в картине, получающейся на длине волны 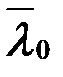 . Поскольку для m -го максимума λ0
. Поскольку для m -го максимума λ0
 ,
,
то, пренебрегая зависимостью 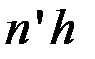 от длины волны, получаем
от длины волны, получаем
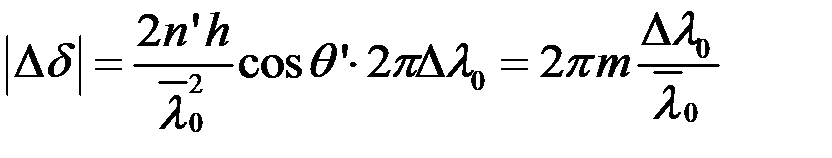 .
.
Если потребовать выполнения условия 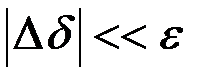 , то, с учетом (8.27), получим
, то, с учетом (8.27), получим
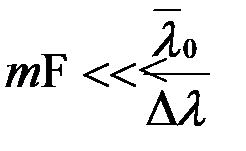 ,
,
и, поскольку оптическая разность хода между соседними интерферирующими пучками для m- го максимума длины волны λ0
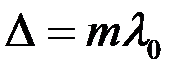 ,
,
получаем:
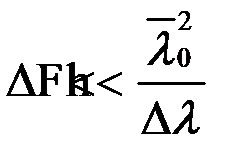 .
.
Это неравенство аналогично выражению (8.9), полученному для двухлучевой интерференции, где в правой части величина тождественна длине когерентности света.
Таким образом, мы показали, что, в отличие от двулучевой интерференции, при многолучевой интерференции происходит более четкое разделение полос. Увеличение коэффициента отражения ρ можно обеспечить либо увеличением угла падения 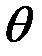 , либо нанесением на поверхность диэлектрических или металлических отражающих покрытий. В последнем случае, ввиду наличия поглощения в металлических пленках, определяемого коэффициентом поглощения α, следует учесть, что
, либо нанесением на поверхность диэлектрических или металлических отражающих покрытий. В последнем случае, ввиду наличия поглощения в металлических пленках, определяемого коэффициентом поглощения α, следует учесть, что
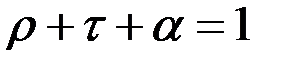 .
.
Тогда соотношение между интенсивностями 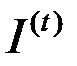 и
и 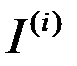 примет вид
примет вид
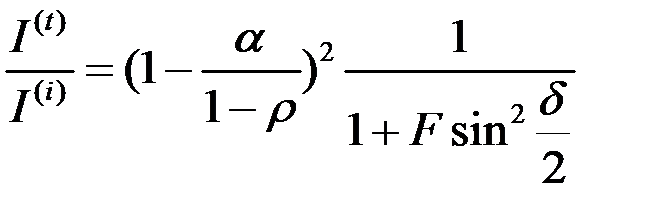 .
.
 2020-04-12
2020-04-12 213
213








