Определение и свойства линейного пространства

Линейные пространства.

Возвращаясь к основным задачам для линейных систем, напомним, что существование и единственность решения доказаны лишь для частного случая квадратных систем с отличным от нуля определителем (для крамеровских систем). Получить аналогичный результат для общей линейной системы и ответить на остальные вопросы, сформулированные в лекции 1, мы сможем, опираясь на понятие линейного пространства, которое и введём в этой лекции.

Линейные операции – сложение и умножение на число – могут выполняться над различными по природе объектами: числами, векторами, функциями, матрицами и т.д. Отвлечёмся от конкретной природы объектов и от привычного способа сложения и умножения на число, а также допустим в качестве множителей любые (не только вещественные) числа из некоторого числового поля . Сохраняя единую точку зрения на линейные операции и их свойства, приходим к понятию линейного пространства.

Множество элементов любой природы называется линейным пространством над полем , если выполняются следующие требования:

1. Имеется правило, по которому ставится в соответствие элемент , называемый суммой элементов , и обозначаемый .

2. Имеется правило, по которому 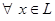и ставится в соответствие элемент 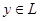, называемый произведением элемента на число и обозначаемый .

3. Эти правила подчинены аксиомам:

1°. - коммутативность суммы,

2°. - ассоциативность суммы,

3°. 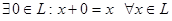- существование нуля и его особая роль при сложении,

4°. - существование противоположного элемента,

5°. - особая роль числового множителя ,

6°. 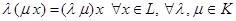- ассоциативность относительно числовых множителей,

7°. - дистрибутивность относительно суммы числовых множителей,

8° 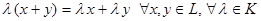- дистрибутивность относительно суммы элементов.

Приведём примеры конкретных линейных пространств.

Пример 1. Пространство 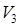- множество векторов в трехмерном пространстве (вернее, множество радиус-векторов точек этого пространства). В 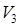определены и операция сложения векторов - по правилу параллелограмма, и операция умножения вектора на вещественное число - «растяжение» в раз с изменением направления при 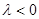. Справедливость всех аксиом устанавливается в курсе аналитической геометрии. Аналогичные множества на плоскости и на прямой будем обозначать и .

Но множество векторов, заполняющих не всю плоскость, а, например, только первую четверть, не образует линейного пространства, так как такое множество не содержит противоположных векторов. Не образуют линейного пространства и векторы на плоскости с выколотым началом координат или на плоскости с прямолинейной щелью, проходящей через начало координат (почему?).

Пример 2. Пространство - множество элементов, каждый из которых определяется совокупностью чисел из некоторого поля : . Числа называются координатами элемента . Операции сложения элементов и умножения элемента на число определяются так:

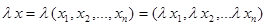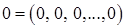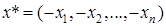Нулевой элемент - совокупность нулей: . Противоположным для элемента является элемент . Легко проверить, что все аксиомы выполняются. Пространство называется -мерным координатным пространством.

Пример 3. Пространство - множество функций , непрерывных на сегменте . Сложение функций и умножение на число производится по правилам анализа, нулевой элемент - это тождественно равная нулю функция. Выполнение аксиом 1° - 8° очевидно.

Пример 4. Пространство - множество многочленов степени, не превышающей , с обычными операциями сложения многочленов и умножения их на число.

Но если все коэффициенты многочлена положительны, то линейного пространства не получим (почему?).

Образует ли линейное пространство множество многочленов строго фиксированной степени n?

Пример 5. Пространство 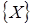- множество всех положительных вещественных чисел. Сумму элементов 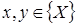определим как произведение этих чисел (тогда нулевой элемент - число 1), произведение элемента на вещественное число 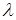определим ка степень (тогда противоположный элемент - это число . Предлагаем убедиться в справедливости аксиом 1° - 8° для такого пространства.

Пример 6. Замечательный пример линейного пространства даёт совокупность всех цветов. Под суммой двух цветов понимаем их смешение, под умножением цвета на положительное число 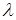- увеличение в 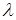раз его интенсивности, под умножением на - дополнительный цвет. Свойства этого линейного пространства используются в цветных телевизорах.

Пример 7. Совокупность всех матриц образует линейное пространство (почему?)

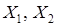Пример 8. Рассмотрим однородную линейную систему, в матричной записи это . Пусть столбцы - два решения этой системы. Свойства умножения матриц позволяют записать

т.е. решения однородной линейной системы можно складывать. Аналогично, если - решение системы и , то

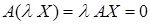
Значит, решение можно умножать на число 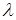. Нулевой элемент - это тривиальное решение, которым всегда обладает однородная система. Поэтому множество решений линейной однородной системы образует линейное пространство (с этим пространством мы ещё встретимся).

Пример 9. Из курса дифференциальных уравнений: совокупность решений линейного однородного дифференциального уравнения образует линейное пространство.

В каждом рассмотренном примере речь идёт о линейных операциях, определённых на некотором множестве, а вот на каком именно - совершенно не имеет значения. Совсем как у Алисы из страны чудес: “Ты видела когда-нибудь, как рисуют множество? - Множество чего? - спрашивает Алиса. - Ничего. Просто множество” Автор этих слов - математик Чарльз Лутвидж Доджсон (Льюис Кэррол), объектом исследований которого были системы линейных уравнений.

Отметим некоторые свойства линейных пространств, являющихся логическими следствиями аксиом 1° - 8°.

Теорема. Во всяком линейном пространстве

1) существует единственный нулевой элемент;

2) для существует единственный противоположный элемент;

3) нулевой элемент равен произведению на число 0;

4) для противоположный элемент равен .

Докажем первое утверждение. Аксиома 3° устанавливает существование нулевого элемента во всяком линейном пространстве . Предположим, что в существуют два нулевых элемента: и 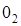. Полагая в аксиоме 3° сначала , , а затем , а , получим:

.¨

Доказательство остальных утверждений предлагаем провести самостоятельно.

Линейное пространство над полем вещественных чисел называют вещественным линейным пространством и обозначают 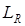. Соответственно - комплексное линейное пространство (над полем комплексных чисел ). Элементы линейного пространства обычно называют векторами (независимо от их природы).

Линейная зависимость

Пусть - произвольное линейное пространство. Перенесём в него знакомое из векторной алгебры понятие линейной зависимости векторов.

Определение. Векторы 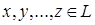называются линейно зависимыми, если существуют такие числа , не все одновременно равные нулю, что линейная комбинация данных векторов с этими числами даёт нулевой вектор пространства :

(1)

Векторы 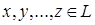называются линейно независимыми, если равенство (1) выполняется только при .

Предлагается в качестве упражнения доказать следующие утверждения:

1. Наличие нулевого вектора в системе влечёт линейную зависимость всей системы;

2. Наличие линейно зависимой подсистемы влечёт линейную зависимость всей системы;

3. Линейная независимость системы наследуется любой её подсистемой;

4. Если векторы линейно независимы, а вектор есть их линейная комбинация 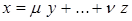, то это представление единственно;

5. Векторы линейно зависимы тогда и только тогда, когда один из них является линейной комбинацией остальных;

6. Верно ли утверждение: в случае линейной зависимости системы каждый вектор является линейной комбинацией остальных?

Рассмотрим несколько примеров.

Пример 1. Показать, что в пространстве ( -мерном координатном пространстве) векторы

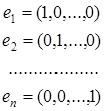(2)

линейно независимы.

Решение. Действительно, линейная комбинация векторов (2) с числами в силу аксиом линейного пространства представляет собой вектор , который является нулевым лишь при условии . ♦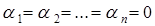

Пример 2. Рассмотреть вопрос о линейной зависимости в -мерном координатном пространстве произвольных векторов

(3)

Решение. Равенство нулю линейной комбинации этих векторов с числами

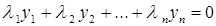, (4)

записанное в координатной форме, приводит к однородной системе линейных уравнений относительно неизвестных :

. (5)

Однородная система (5) всегда имеет тривиальное решение

Если тривиальное решение является единственным, т.е. система (5) - а с ней и равенство (4) - удовлетворяется только с нулевым набором чисел , то векторы линейно независимы. Если же система (5) нетривиально совместна, т.е. кроме тривиального существует решение

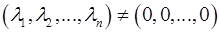то векторы линейно зависимы. Иначе: линейная зависимость векторов в пространстве и нетривиальная совместность однородной системы линейных уравнений с неизвестными - это две стороны одной медали. ♦

Пример 3. Показать, что в пространстве 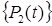многочленов, степень которых не выше 2, простейший набор линейно независимых векторов - это векторы .

Решение. Действительно, линейная комбинация даёт тождественно равный нулю многочлен лишь при . ♦

Пример 4. Убедиться, что в пространстве многочленов, степень которых не выше , простейший набор линейно независимых векторов – это (всего векторов). ♦