Базис и размерность линейного пространства

Рассмотрим линейное пространство над полем .

Определение. Векторы образуют базис в , если они

1) линейно независимы;

2) 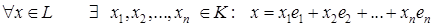. (6)

Равенство (6) - это разложение вектора по базису , числа - координаты вектора в базисе . Координаты вектора в данном базисе определяются однозначно, доказательство этого важного утверждения основано на определении линейно независимых векторов.

Главное значение базиса: линейные операции над объектами произвольной природы (которые мы лишь для удобства называем векторами) сводятся к соответствующим операциям над числами - координатами векторов в данном базисе. Действительно, из аксиом 1° - 8° следует

Теорема. При сложении двух векторов произвольного линейного пространства их координаты относительно данного базиса складываются; при умножении вектора на число все его координаты умножаются на это число.

Например, в линейном пространстве любая тройка некомпланарных векторов образует базис; в 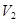базис образует любая пара неколлинеарных векторов.

В пространстве базис образуют векторы (2): их линейная независимость была установлена выше, а представление для очевидно.

В пространстве базис образуют линейно независимые векторы . Действительно, всякий многочлен степени не выше второй может быть записан в виде . Здесь координаты многочлена 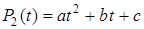в базисе суть числа .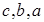

В пространстве цветов базисными являются три цвета - красный, синий и жёлтый (или красный, синий и зелёный), с помощью линейных комбинаций которых можно получить любой цвет спектра.

Определение. Число называется размерностью линейного пространства , если в этом пространстве

1) существует линейно независимых векторов,

2) любые векторов линейно зависимы.

Иначе: размерность линейного пространства - это максимальное количество линейно независимых векторов в . Обозначается размерность пространства символом (от английского dimension). Например, в 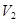максимальное количество линейно независимых векторов - два (любые три вектора на плоскости линейно зависимы), значит, . Аналогично, (любые четыре вектора линейно зависимы).

Определение. Линейное пространство называется бесконечномерным, если в нём существует любое число линейно независимых векторов.

Бесконечномерным является функциональное пространство , в котором существуют линейно независимые векторы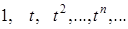

Естественно, понятия базиса и размерности линейного пространства тесно связаны, а именно, справедлива

Теорема. Если , то в существует базис из n векторов. И обратно: если в существует базис из n векторов, то .

Доказательство.

1. Пусть . Тогда, во-первых, существуют линейно независимых векторов , во-вторых, если к ним добавить 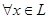, то система векторов линейно зависима. Это значит, что справедливо равенство

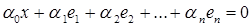, (7)

причём число заведомо отлично от нуля (иначе бы равенство (7) означало линейную зависимость векторов ). При из равенства (7) следует

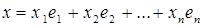
Здесь обозначено 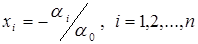. Значит, линейно независимые векторы являются, по определению, базисом.

2. Пусть векторы образуют базис, т.е. они линейно независимы. Для доказательства утверждения остаётся показать, что любая система из векторов линейно зависима.

Разложим каждый из векторов по базису :

Составим из коэффициентов матрицу

размерность которой , значит, . Поэтому строки матрицы (а с ними и векторы линейно зависимы.¨

Например, в координатном пространстве базисом является система (2) из векторов[m1], значит, .

В пространстве многочленов степени не старше 2 базис образуют три вектора , значит, . Аналогично .

Предлагается самостоятельно найти

1) размерность и базис пространства всех матриц;

2) координаты многочлена в базисе 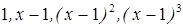. Указание: разложить многочлен по формуле Тейлора в окрестности точки (т.е. по степеням .

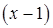Подпространства

Совокупность векторов линейного пространства называется подпространством, если результат линейных операций с этими векторами остаётся в ,. иначе, выполняются условия:

1° ;

2° .

Докажем, что такая совокупность сама является линейным пространством. Для этого достаточно проверить справедливость аксиом 1° – 8° для векторов из . Но аксиомы 1°, 2°, 5° – 8° заведомо выполняются в , поскольку они имеют место для всех векторов из . Осталось проверить аксиомы 3° и 4°, т.е. убедиться, что в существует нулевой вектор и для существует противоположный вектор. Возьмём и . По определению подпространства вектор . Остаётся заметить, что по свойствам линейного пространства вектор при превращается в нулевой вектор, а при 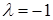он превращается в противоположный для вектор. ¨

Наименьшее возможное подпространство линейного пространства – это нуль-вектор, наибольшее возможное подпространство пространства – само пространство . Эти подпространства обычно называют тривиальными.

Приведём примеры нетривиальных подпространств:

1) В пространстве 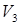все векторы, лежащие в какой-нибудь плоскости (на прямой), проходящей через начало координат, образуют подпространство , т.е. .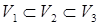

2) Пространство многочленов степени не старше (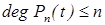) есть подпространство функционального пространства 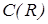- множества непрерывных на действительной оси функций: .

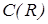3) Напомним, что решения

однородной линейной системы можно складывать и умножать на число. Пространство (множество решений однородной системы уравнений с неизвестными) является подпространством -мерного координатного пространства :

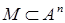
Нам ещё предстоит определить размерность этого подпространства и построить в нём базис, после чего мы сумеем записать любой вектор 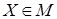(любое решение однородной системы ).

Зададим линейное пространство и некоторое его подпространство 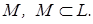Из определения подпространства следует, что . Пусть в выбран базис . Вообще говоря, нельзя из базисных векторов пространства выбрать базисные векторы подпространства , хотя бы потому, что в может не входить ни один из них. Например, в выберем базис – любую пару 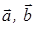неколлинеарных векторов. Проведем прямую, лежащую в одной плоскости с 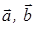и имеющую с ними только одну общую точку. Множество векторов на этой прямой образует подпространство . Очевидно, что ни один из векторов 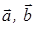не может быть базисным в , т.к. ни один из них не лежит на этой прямой. Но если выбран базис в подпространстве , то его всегда можно дополнить до базиса во всём пространстве . Попробуйте доказать это утверждение.