Вводя определенный интеграл как предел интегральных сумм, мы предполагали, что отрезок интегрирования конечный, а подынтегральная функция ограничена на этом отрезке. Если хотя бы одно из этих условий не выполнено, то данное выше определение определенного интеграла теряет смысл. Так, в случае бесконечного отрезка интегрирования нельзя разбить отрезок на п частей конечной длины, а в случае неограниченной функции интегральная сумма не имеет конечного предела. Однако и в этих случаях удается обобщить понятие определенного интеграла. В результате такого обобщения и появилось понятие несобственного интеграла.
Несобственные интегралы с бесконечными пределами интегрирования
Определение. Пусть функция 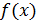 определена в промежутке
определена в промежутке 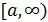 и интегрируема в любой его части
и интегрируема в любой его части 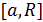 , т. е. существует определенный интеграл при любом
, т. е. существует определенный интеграл при любом 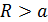 . Тогда, если существует конечный предел
. Тогда, если существует конечный предел

то его называют несобственным интегралом первого рода и обозначают символом
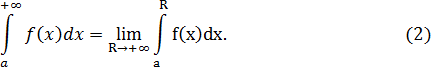
В этом случае говорят, что интеграл (2) существует или сходится. Если же предел (1) не существует или бесконечен, то говорят, что несобственный интеграл не существует или расходится.
Аналогично интегралу (2) вводится несобственный интеграл вида
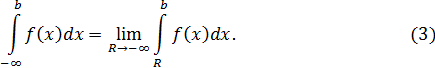
Наконец, как сумму подобных интегралов можно определить несобственный интеграл с обоими бесконечными пределами, т. е. определить его равенством
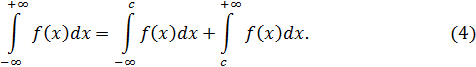
где 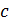 — любое число; при условии существования обоих интегралов справа,
— любое число; при условии существования обоих интегралов справа,
Легко установить геометрический смысл несобственного интеграла первого рода. Пусть 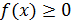 . Тогда, если определенный интеграл
. Тогда, если определенный интеграл
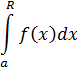
выражает площадь области, ограниченной сверху графиком функции 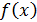 , снизу осью
, снизу осью 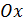 , слева прямой
, слева прямой 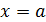 , справа прямой
, справа прямой 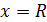 , то естественно считать, что несобственный интеграл
, то естественно считать, что несобственный интеграл
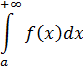
выражает конечную площадь бесконечной области, ограниченной снизу осью 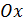 , сверху графиком функции
, сверху графиком функции 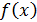 , слева прямой
, слева прямой 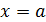 (см. рис.).
(см. рис.).
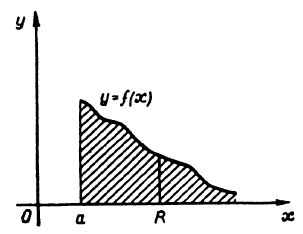
Аналогичные рассуждения имеют место для интегралов (3) и (4).
Рассмотрим несколько примеров несобственных интегралов первого рода.
Пример 1.
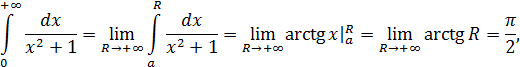
т. е. данный интеграл сходится.
Пример 2.
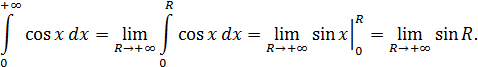
а предел функции 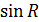 при
при 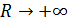 не существует, следовательно, интеграл расходится.
не существует, следовательно, интеграл расходится.
Заметим, что в рассмотренных примерах само вычисление несобственного интеграла основано на его определении.
 2020-04-12
2020-04-12 101
101







