Определение. Пусть функция 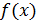 определена в промежутке
определена в промежутке  . Точку
. Точку  будем называть особой, если функция
будем называть особой, если функция 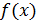 не ограничена в окрестности этой точки, но ограничена на любом
не ограничена в окрестности этой точки, но ограничена на любом  , заключенном в
, заключенном в  (см. рис.).
(см. рис.).

Предполагается, что на любом  , функция
, функция 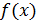 интегрируема. Тогда, как бы ни было мало
интегрируема. Тогда, как бы ни было мало  , если существует конечный предел
, если существует конечный предел 

то его называют несобственным интегралом второго рода и обозначают 





В этом случае говорят, что интеграл (6) существует или сходится. Если же предел (5) не существует или бесконечен, то говорят, что интеграл (6) не существует или расходится.
Аналогично, если точка 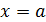 — особая точка, то несобственный интеграл в этом случае определяется так:
— особая точка, то несобственный интеграл в этом случае определяется так:

Если 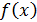 не ограничена в окрестности какой-нибудь внутренней точки
не ограничена в окрестности какой-нибудь внутренней точки  , то по определению полагают
, то по определению полагают

при условии существования обоих интегралов справа.
Наконец, если  и
и  — особые точки, то в этом случае несобственный интеграл определяется как сумма
— особые точки, то в этом случае несобственный интеграл определяется как сумма

где 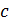 — любая точка из
— любая точка из  , если оба интеграла справа существуют.
, если оба интеграла справа существуют.
Пример.

а при 

таким образом, данный интеграл сходится при  и расходится при
и расходится при 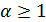 .
.
Признаки сходимости несобственных интегралов. Рассмотрим вопрос сходимости интегралов с бесконечными пределами интегрирования вида
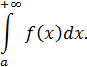
Аналогичные рассуждения можно провести и для интегралов других видов.
Следующая теорема познакомит нас с одним из признаков сходимости несобственных интегралов.
Теорема 11 (признак сравнения несобственных интегралов). Если функции  и
и 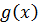 непрерывны на полуинтервале
непрерывны на полуинтервале  и удовлетворяют на нем условию
и удовлетворяют на нем условию  , то из сходимости интеграла
, то из сходимости интеграла

следует сходимость интеграла

а из расходимости интеграла (8) следует расходимость интеграла (7).
Доказательство. Так как интеграл (7) по условию сходится, то согласно теореме об ограниченности сходящейся последовательности (сходящаяся последовательность ограничена) это означает, что существует число  такое, что для любого
такое, что для любого 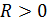 выполняется неравенство
выполняется неравенство

Тогда, в силу данного условия и оценки 2°

А это означает, что функция
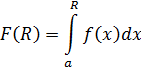
Монотонно возрастает и ограничена, т. е. имеет конечный предел при 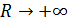 , и, следовательно, интеграл (8) сходится.
, и, следовательно, интеграл (8) сходится.
Если же (8) расходится, то, допустив сходимость интеграла (7), получим по только что доказанному сходимость интеграла (8), что противоречит условию. Окончательно получаем, что интеграл (7) также расходится.
Замечание. Что касается сходимости несобственных интегралов второго рода, то теория этих интегралов аналогична теории несобственных интегралов первого рода. В частности, признак сравнения для таких интегралов можно сформулировать следующим образом: если функции 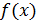 и
и  непрерывны на полуинтервале
непрерывны на полуинтервале 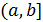 и для всех точек
и для всех точек  в некоторой окрестности точки а выполняются условия
в некоторой окрестности точки а выполняются условия  , то из сходимости интеграла
, то из сходимости интеграла  следует сходимость интеграла
следует сходимость интеграла  , а из расходимости
, а из расходимости  следует расходимость
следует расходимость  .
.
Пример. Исследовать сходимость

Специальный признак сходимости. Если 1) функция  монотонно стремится к 0 при
монотонно стремится к 0 при  и 2) функция
и 2) функция 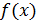 имеет ограниченную первообразную
имеет ограниченную первообразную

то интеграл

сходится, вообще говоря. не абсолютно.
В частности, интегралы
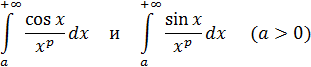
сходятся, если  .
.
 2020-04-12
2020-04-12 199
199







