2020-04-12
153МАТЕМАТИКА
Тема 91-92: «Иррациональные уравнения»
Цели:
- изучить методы решения иррациональных уравнений;
- рассмотреть различные примеры их применения;
- развивать умение наблюдать, обобщать, классифицировать, анализировать математические ситуации.
Продолжительность занятия - 2 часа
Оборудование: карточки с заданиями, чертежные инструменты, ручка, тетрадь
Краткие теоретические сведения:
Краткое обсуждение тех теоретических знаний, которыми они обладают и пользуются при решении иррациональных уравнений.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня.
Иррациональное уравнение, как правило, сводится к равносильной системе, содержащей уравнения и неравенства.
1. 
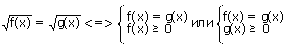
Из двух систем выбирают ту, которая решается проще.
2. 
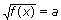
Если а < 0, уравнение не имеет корней.
Если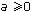 
, уравнение равносильно уравнению 
.
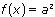3. 
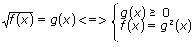
Иррациональные уравнения могут быть также решены путем возведения обеих частей уравнения в натуральную степень. При возведении уравнения в степень могут появится посторонние корни. Поэтому необходимой частью решения иррационального уравнения является проверка.
При решении иррациональных уравнений, как правило, используют следующие методы:
1) переход к равносильной системе (в этом случае проверка не нужна);
2) метод возведения обеих частей уравнения в одну и ту же степень;
3) метод введения новых переменных.
Если вы не следите за равносильностью переходов, то проверка является обязательным элементом решения. О.Д.З. в иррациональных уравнениях не поможет Вам отсеять все посторонние корни. Обратите на это внимание!
При решении иррациональных уравнений, как правило, используют следующие методы: 1) переход к равносильной системе (в этом случае проверка не нужна); 2) метод возведения обеих частей уравнения в одну и ту же степень; 3) метод введения новых переменных.
Пример 1.
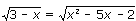
Решение:
|
| <=> | 
| <=> | 
| <=> | 
| <=> |
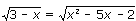
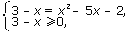
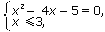
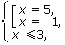
| <=> x = -1 |
Ответ: -1.
Пример 2.
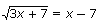
Решение:
|
| <=> | 
| <=> | 
| <=> |
| <=> | 
| <=> | 
|
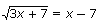
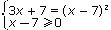
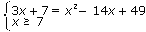
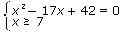
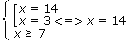
Ответ: 14.
Пример 3.
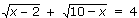
Решение: ОДЗ:
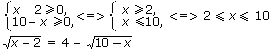
Возведем обе части уравнения в квадрат:
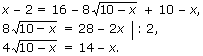
Возведем обе части уравнения в квадрат:
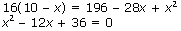
х = 6 входит в ОДЗ, значит может быть корнем данного уравнения.
Проверка:
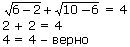
Ответ: 6
Пример 4.
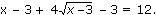
Решение: ОДЗ: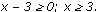 
Обозначим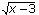 
= у. Тогда х-3=у2.
у2 + 4у - 12 = 0;
у1 = -6, у2 = 2.
а) 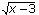=-6. Решений нет, т.к. -6>0, а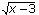 
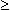0.
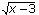б) = 2,
х - 3 = 4,
х = 7 входит в ОДЗ.
Ответ: 7.
Домашнее задание:
Сделать конспект по теме, решить уравнения и оформить их решение:
а)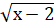 
+ 
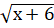= 4
б) 
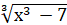= 1
Список литературы:
Алгебра и начала математического анализа, автор Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева, учебник для общеобразовательных организаций, базовый и углубленный уровни, 5 издание, Москва «Просвещение», 2019г.
Преподаватель - Брыкало А.А., brukalo_aa@mail.ru
