Произвольный треугольник

Радиус описанной окружности: R =(a ⋅ b ⋅ c)/( 4⋅ S Δ);

R = a/( 2 sinα), где α — угол, противолежащий стороне a;

Радиус вписанной окружности: r = S Δ/ p, где p — полупериметр.

105. Если все стороны четырёхугольника касаются окружности, то он называется четырёхугольником, описанным около этой окружности, а окружность — вписанной в четырёхугольник.

Не все четырёхугольники возможно описать около окружности, так как биссектрисы четырёх углов могут не пересекаться в одной точке, и не удастся найти центр вписанной окружности.

106. Если суммы противоположных сторон четырёхугольника равны, то в такой четырёхугольник можно вписать окружность.

Суммы противоположных сторон описанного четырёхугольника равны АД+ВС=АВ+СД

107. Четырёхугольник, все вершины которого лежат на окружности, называется вписанным в эту окружность, а окружность называется описанной около четырёхугольника.

Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.

108. Вектор можно обозначить:

- двумя заглавными буквами, поставив над ними стрелочку; первая буква показывает начальную точку, вторая — конечную точку, например, A¯B (читается: вектор AB);
- маленькой буквой со стрелочкой над ней, например, a ⃗ (читается: вектор a).

Если начальная и конечная точки вектора совпадают, получается нулевой вектор, который обозначается как 0⃗. Любую точку на плоскости можно считать нулевым вектором.

Длина отрезка AB называется длиной, или модулем, вектора AB и обозначается так: ∣ AB ∣.

109. Скалярными называют величины, имеющие численное значение, но не имеющие направления.

Примеры — количество каких-нибудь предметов, длина, плотность.

110. Векторными величинами, или векторами, называют величины, имеющие и численное значение, и направление. Примеры векторных величин — скорость, сила, перемещение.

111. Перемещением движущейся точки в данный момент времени называют вектор с началом в точке начала её движения и концом в точке её расположения в этот момент.

Векторными величинами, или векторами, называют величины, имеющие и численное значение, и направление.

Например, если сказано, что автомобиль движется со скоростью 100 километров в час (то есть, дано численное значение скорости), то про его скорость известно не всё, потому что неизвестно, куда, в каком направлении он двигается. Поэтому примеры векторных величин — скорость, сила, перемещение.

112. Запомни различие между расстоянием и перемещением.

Расстояние характеризуется только числовым значением, например, AB + BC + CD =5 км.

Расстояние — скалярная величина.

Перемещение — вектор AD, соединяющий начальное и конечное положение тела, и его длина не равняется 5 км.

Перемещение — векторная величина.

Например, можно проехать 5 км и вернуться обратно, перемещение же в этом случае будет равно 0 и обозначится как нулевой вектор.

113. Два отличных от нуля вектора, которые находятся на одной прямой или параллельных прямых, называются коллинеарными векторами.

114. Два коллинеарных вектора могут быть направлены в одном направлении или в противоположных направлениях. В первом случае коллинеарные векторы называются сонаправленными, а во втором — противоположно направленными векторами.

Сонаправленные векторы записываются a ⃗ ↑↑ b ⃗ или b ⃗ ↑↑ a ⃗;
противоположно направленные векторы записываются
a ⃗ ↑↓ b ⃗ или b ⃗ ↑↓ a ⃗.

115. Векторы с равными модулями и одинаковыми направлениями называются равными векторами.

116. Векторы с равными модулями и противоположными направлениями называются противоположными векторами.

117. Противоположные векторы a ⃗ и b ⃗ записываются так: a ⃗ =− b ⃗ или b ⃗ =− a ⃗.

Меняя направление какого-либо вектора на противоположное, получаем вектор, противоположный данному: AB =− BA

118. Даны векторы a ⃗ и b ⃗. Если векторы a ⃗ и b ⃗ отложить последовательно друг за другом (начало вектора b ⃗ попадает в конец вектора a ⃗), то вектор суммы c ⃗ соединяет начало одного вектора с концом второго вектора.

a ⃗ + b ⃗ = c ⃗ Такой приём сложения векторов называется правилом треугольника.

119. Даны векторы a ⃗ и b ⃗. Если векторы a ⃗ и b ⃗ исходят из одной точки, то вектор суммы c ⃗ исходит из общей начальной точки векторов и является диагональю параллелограмма, сторонами которого являются векторы a ⃗ и b ⃗.

Запись:

a ⃗ + b ⃗ = c ⃗ или AB + AD = AC.

Такой приём сложения векторов называется правилом параллелограмма.

120. Законы сложения векторов:

1) Для любых двух векторов a ⃗ и b ⃗ в силе равенство a ⃗ + b ⃗ = b ⃗ + a ⃗ (коммутативный, или переместительный, закон сложения).

2) Для любых трёх векторов a ⃗, b ⃗, c ⃗ в силе равенство (a ⃗ + b ⃗)+ c ⃗ = a ⃗ +(b ⃗ + c ⃗) (ассоциативный, или сочетательный, закон сложения).

121. Сумму нескольких векторов получаем так: складываем первый и второй вектор, затем к их сумме прибавляем третий вектор и т. д.

Из закона сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются. Это правило многоугольника.

122. Чтобы лучше понять закон вычитания векторов, нужно вспомнить свойство математических действий: сложения и вычитания.

Если x + y = z, то x = z − y.

Такое же свойство справедливо и для действий с векторами.

Чтобы вычесть вектор b ⃗ из вектора a ⃗, нужно найти такой вектор c ⃗, сумма которого с вектором b ⃗ составляла бы вектор a ⃗.

123. Легче запомнить, как найти разность векторов a ⃗ и b ⃗, следующим образом:

1) векторы нужно привести к общему началу A;

2) соединить конечные точки B и C;

3) отметить направление вектора разности от конечной точки уменьшителя к конечной точке уменьшаемого вектора.

124.

125.

126. Произведением вектора a ⃗ на число k (k ≠0) называется вектор b ⃗, модуль которого равен ∣∣ b ⃗ ∣∣=| k |⋅| a ⃗ |, при этом:

- векторы a ⃗ и b ⃗ сонаправлены, если k >0;

- векторы a ⃗ и b ⃗ противоположно направлены, если k <0.

127. Если умножить вектор на число 1, получим равные векторы.

Если умножить вектор на число −1, получим противоположные векторы.

128. Расстояние между двумя точками

Как известно, координаты вектора можно определить, если даны координаты начальной и конечной точек вектора A (x 1; y 1) и B (x 2; y 2).

AB (x 2− x 1; y 2− y 1).

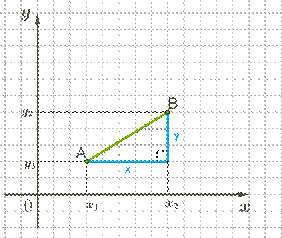
129. Координаты середины отрезка

Если даны координаты конечных точек отрезка, знания о действиях с векторами и координатами векторов дают возможность определить координаты серединной точки отрезка.

Для этого расположим отрезок AB в системе координат.

A (x 1; y 1), B (x 2; y 2) — конечные точки отрезка с данными координатами.

C (x; y) — серединная точка с искомыми координатами.

Пусть векторы OA, OB и OC − начнутся в начале координат, в таком случае их координаты совпадут с координатами их конечных точек.

Если сосчитать векторы OA и OB по закону параллелограмма, тo OC =1/2(OA + OB).

Kак известно, в координатной форме координаты суммы находим как сумму координат слагаемых векторов, а при умножении с числом координаты находим умножением координат.

Следовательно, OC {(x 1+ x 2)/2;(y 1+ y 2)/2}, т о есть искомые значения x и y:

x =(x 1+ x 2)/2; y =(y 1+ y 2)/2.

ТРЕУГОЛЬНИК

в нешний угол СВД = ; К – точка пересечения высот (ортоцентр треугольника). h_a, h_b, h_c – высоты треугольника на соответствующие стороны.

где полупериметр .

М – точка пересечения медиан треугольника (центр тяжести).

m_a, m_b, m_c – медианы на соответствующие стороны. МВ:МД=МА:МЕ=МС:МК=2/1

Т – точка пересечения биссектрис треугольника (центр вписанной окружности). L_a, L_b, L_c – биссектрисы соответствующих углов. ВМ:МС = АВ:АС

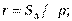
r – радиус вписанной окружности. О – точка пересечения серединных перпендикуляров к сторонам треугольника (центр описанной окружности). Радиус описанной окружности:

где S_Δ – площадь треугольника; p – периметр треугольника; h_c –

высота опущенная на соответствующую сторону с. На всех 4–х нарисованных треугольниках стороны одинаково обозначены, просто на 1–м они обозначены, а на остальных они опущены для упрощения рисунка. И вообще подразумевается, что все 4 треугольника абсолютно одинаковые.

M N – средняя линяя треугольника. MN=0.5AC; MN║AC.