Скалярное поле и его характеристики
1. Найти производную функции 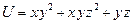 в точке
в точке 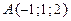 в направлении
в направлении 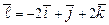 .
.
Указать характер изменения скалярного поля в данном направлении.
Ответ: 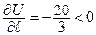
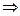 скалярное поле в направлении вектора
скалярное поле в направлении вектора 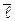 в точке
в точке 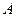 убывает.
убывает.
2. Найти производную функции 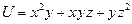 в точке
в точке 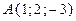 в направлении вектора
в направлении вектора 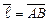 ,
,
где 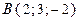 . Указать характер изменения скалярного поля в направлении вектора
. Указать характер изменения скалярного поля в направлении вектора 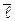 .
.
Ответ: 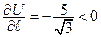
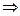 скалярное поле в направлении вектора
скалярное поле в направлении вектора 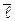 в точке
в точке 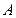 убывает.
убывает.
3. Найти скорость и направление быстрейшего возрастания функции 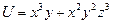 в точке
в точке
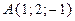 .
.
Ответ: 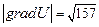 - скорость быстрейшего возрастания скалярного поля в точке
- скорость быстрейшего возрастания скалярного поля в точке 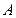 ;
;
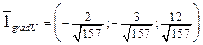 - направление быстрейшего возрастания скалярного поля в точке
- направление быстрейшего возрастания скалярного поля в точке 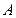 .
.
4. Найти производную функции 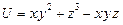 в точке
в точке 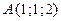 в направлении, образующем с
в направлении, образующем с
осями координат острые углы 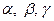 , если
, если 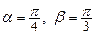 .
.
Ответ: 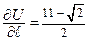 .
.
5. Найти производную функции 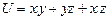 в точке
в точке 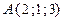 в направлении вектора
в направлении вектора 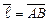 ,
,
где 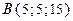 . Указать характер изменения скалярного поля в данном направлении.
. Указать характер изменения скалярного поля в данном направлении.
Ответ: 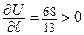
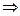 скалярное поле в направлении вектора
скалярное поле в направлении вектора 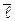 в точке
в точке 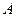 возрастает.
возрастает.
6. Найти производную функции 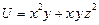 в точке
в точке 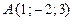 в направлении
в направлении 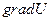 .
.
Ответ: 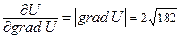 .
.
7. Найти производную скалярного поля 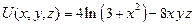 в точке
в точке 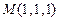 в направлении
в направлении
вектора 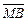 , где
, где 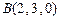 . Сделать вывод о поведении поля.
. Сделать вывод о поведении поля.
Ответ: 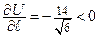
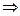 скалярное поле в направлении вектора
скалярное поле в направлении вектора 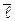 =
= 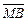 в точке
в точке 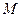 убывает.
убывает.
8. Указать скорость и направление наибыстрейшего возрастания скалярного поля 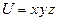
в точке 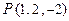 .
.
Ответ: 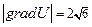 - скорость наибыстрейшего возрастания скалярного поля в точке
- скорость наибыстрейшего возрастания скалярного поля в точке 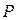 ;
;
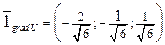 - направление наибыстрейшего возрастания скалярного поля в точке
- направление наибыстрейшего возрастания скалярного поля в точке 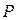 .
.
9. Найти производную скалярного поля 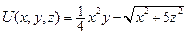 в направлении вектора
в направлении вектора
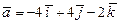 в точке
в точке 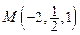 . Сделать вывод о поведении поля.
. Сделать вывод о поведении поля.
Ответ: 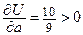
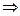 скалярное поле в направлении вектора
скалярное поле в направлении вектора 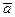 в точке
в точке 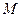 возрастает.
возрастает.
10. Найти производную скалярного поля 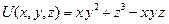 в точке
в точке 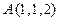 в направлении,
в направлении,
образующим с осями координат углы соответственно 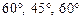 .
.
Ответ: 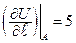 .
.
Криволинейный интеграл I рода (по длине дуги).
Вычисление и приложения
1. Найти массу параболы 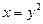 от точки
от точки 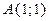 до точки
до точки 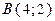 , если плотность в каждой точке
, если плотность в каждой точке
параболы равна ординате этой точки.
Ответ: 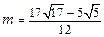 .
.
2. Найти массу дуги линии 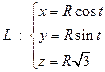 , где
, где 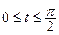 ,
,
если плотность в каждой точке линии 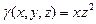 .
.
Ответ: 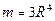 .
.
3. Найти статический момент относительно оси 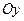 однородной
однородной 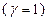 дуги
дуги 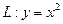 от точки
от точки 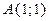
до точки 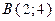 .
.
Ответ: 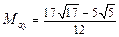 .
.
4. Вычислить 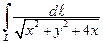 по отрезку прямой
по отрезку прямой 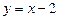 от точки
от точки 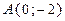 до точки
до точки 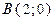 .
.
Ответ: 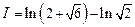 .
.
5. Найти момент инерции относительно начала координат окружности 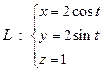 ,
,
если плотность 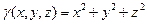 .
.
Ответ: 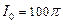 .
.
6. Найти координаты центра тяжести однородной 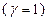 половины окружности
половины окружности 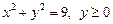 .
.
Ответ: 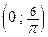 .
.
 2020-04-12
2020-04-12 114
114







