Пусть функция 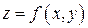 определена в области
определена в области 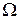 плоскости
плоскости 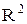 , а
, а 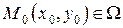 – заданная точка.
– заданная точка.
Определение 2.1. Число 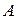 называется пределом функции
называется пределом функции 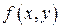 в точке
в точке 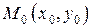 (или при стремлении точки
(или при стремлении точки 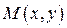 к точке
к точке 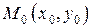 ), если для любого числа
), если для любого числа 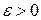 найдется такое число
найдется такое число 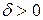 , что для всех точек
, что для всех точек 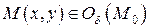 за исключением, быть может, точки
за исключением, быть может, точки 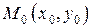 , справедливо неравенство
, справедливо неравенство
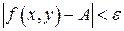 .
.
Если число 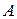 является пределом функции
является пределом функции 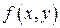 при стремлении точки
при стремлении точки 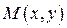 к точке
к точке 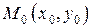 , то пишут
, то пишут
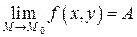 .
.
Основные теоремы о пределах функции одной переменной справедливы и для функций двух и большего числа переменных. Формулировки этих теорем приведем для функций двух переменных.
Теорема 2.1. Предел постоянной величины равен самой постоянной величине.
Если 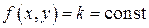 , то
, то
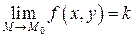 .
.
Будем предполагать, что функции 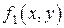 и
и 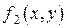 имеют пределы при стремлении точки
имеют пределы при стремлении точки 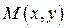 к точке
к точке 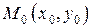 .
.
Теорема 2.2. Предел суммы двух функций равен сумме пределов этих функций:
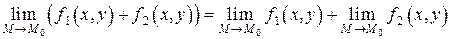 .
.
Теорема 2.2 справедлива для любого конечного числа функций.
Теорема 2.3. Предел разности двух функций равен разности пределов этих функций:
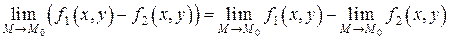 .
.
Из теорем 2.1 – 2.3 вытекает следующее утверждение:
Следствие 2.1. Пусть функции 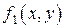 , …,
, …, 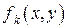 имею пределы при стремлении точки
имею пределы при стремлении точки 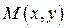 к точке
к точке 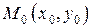 , а
, а 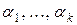 – произвольные постоянные. Тогда имеет место равенство
– произвольные постоянные. Тогда имеет место равенство
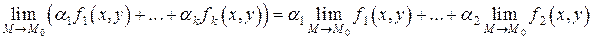 .
.
Теорема 2.4. Предел произведения двух функций равен произведению пределов этих функций:
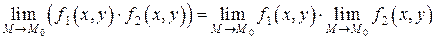 .
.
Теорема 2.5. Предел отношения двух функций равен отношению их пределов:
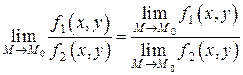 ,
,
если предел знаменателя не равен нулю 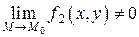 .
.
Пример 2.1. Вычислитьпредел
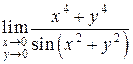 .
.
Решение. Данное выражение представляет неопределенность вида 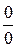 . Так как данное выражение является положительным для всех
. Так как данное выражение является положительным для всех 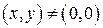 , то
, то
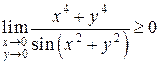 . (*)
. (*)
Так как
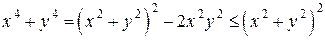 ,
,
то имеем
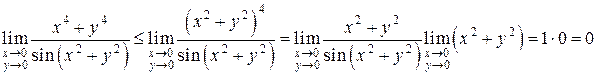 ,
,
то есть
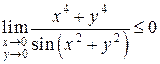 .
.
Отсюда, и из (*) получаем
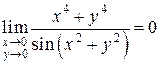 .
.
Пример 2.2. Вычислитьпредел
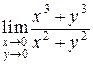 .
.
Решение. Переходим к полярным координатам:
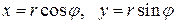 .
.
Тогда 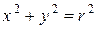 ,
, 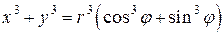 и
и 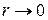 . Так как функция
. Так как функция 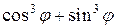 при всех
при всех 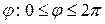 является ограниченной, то имеем
является ограниченной, то имеем
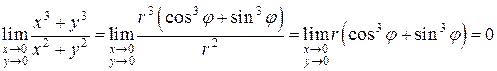 .
.
В некоторых случаях при вычислении предела функции двух переменных используется следующий приём. Полагая 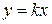 , вместо предела функции двух переменных вычисляют предел функции одной переменной. Если значение предела при некоторых разных значений параметра
, вместо предела функции двух переменных вычисляют предел функции одной переменной. Если значение предела при некоторых разных значений параметра 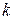 будут различными, то рассматриваемый предел не существует.
будут различными, то рассматриваемый предел не существует.
Пример 2.3. Вычислитьпредел
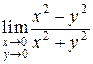 .
.
Решение. Положим 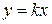 . Тогда
. Тогда
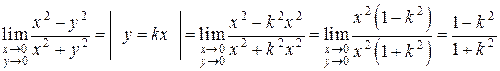 .
.
Так как
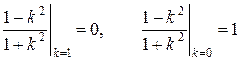 ,
,
и эти значения различны, то рассматриваемый предел не существует.
Замечание. С помощью данного приёма только можно утверждать о не существования предела. Даже в том случае, когда значение предела не будет зависеть от параметра 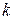 , нельзя утверждать что предел существует и равен значению предела, которого вычислили полагая
, нельзя утверждать что предел существует и равен значению предела, которого вычислили полагая 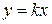 .
.
 2020-04-12
2020-04-12 968
968








