Пусть на множестве  плоскости
плоскости 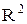 задана функция двух переменных
задана функция двух переменных 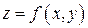 .
.
Определение 3.1. Функция 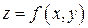 называется непрерывной в точке
называется непрерывной в точке 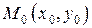 , если:
, если:
1) она определена в точке 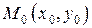 и некоторой ее окрестности;
и некоторой ее окрестности;
2) ее предел при стремлении точки  к точке
к точке 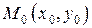 равен значению функции
равен значению функции  в точке
в точке 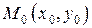
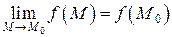 или
или 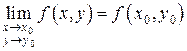 .
.
Определение 3.2. Функция 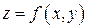 называется непрерывной на множестве
называется непрерывной на множестве  , если она непрерывна в каждой точке этого множества.
, если она непрерывна в каждой точке этого множества.
Определение 3.3. Точка 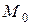 называется точкой разрыва функции
называется точкой разрыва функции  , если в ней нарушено хотя бы одно из условий 1), 2) определения 3.1.
, если в ней нарушено хотя бы одно из условий 1), 2) определения 3.1.
Пример 3.1. Найти точки разрыва функции
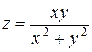 .
.
Решение. Дробная функция не определена в точках, в которых знаменатель обращается в нуль:
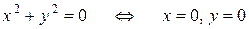 .
.
Данная функция имеет единственную точку разрыва: 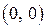 .
.
Пример 3.2. Найти точки разрыва функции
 .
.
Решение. Функция синус определена на всей числовой прямой. Дробная функция не определена в точках, в которых знаменатель обращается в нуль:
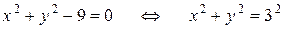 .
.
Все точки окружности радиуса 3 с центром в начале координат являются точками разрыва данной функции.
Свойства функций, непрерывных в ограниченной замкнутой области
Пусть 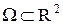 – ограниченная замкнутая область.
– ограниченная замкнутая область.
Теорема 4.1. Если функция 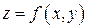 непрерывна в ограниченной замкнутой области
непрерывна в ограниченной замкнутой области  , то она в этой области ограничена, то есть существует число
, то она в этой области ограничена, то есть существует число 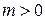 , что
, что
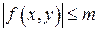
для всех 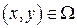 .
.
Теорема 4.2. Если функция 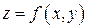 непрерывна в ограниченной замкнутой области
непрерывна в ограниченной замкнутой области  , то она принимает в этой области свое наименьшее и наибольшее значения, то есть если
, то она принимает в этой области свое наименьшее и наибольшее значения, то есть если
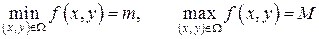 ,
,
то сушествуют точки 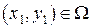 и
и 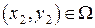 такие, что
такие, что
 .
.
Теорема 4.3. Если функция 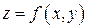 непрерывна в ограниченной замкнутой области
непрерывна в ограниченной замкнутой области  , то она принимает в этой области любое промежуточное значение между
, то она принимает в этой области любое промежуточное значение между 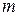 и
и 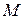 , то есть если
, то есть если 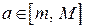 , то существует хотя бы одна точка
, то существует хотя бы одна точка 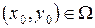 такая, что
такая, что
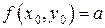 .
.
 2020-04-12
2020-04-12 198
198







