Программирование оптимального управления КА

Необходимо перевести КА из одной точки круговой орбиты с радиусом r₀ в другую, считая при этом, что на КА имеется двигательная установка малой тяги, способная создавать управляющее ускорение по нормали к радиус-вектору.

Исходные уравнения движения заданы в полярной системе координат:

где r – радиус-вектор; φ – угловая полярная координата; V_R, V_T – радиальная и трансверсальная составляющие скорости; μ – гравитационная постоянная Земли: f_T – управляющее ускорение.

Полагая, что в процессе перевода отклонения 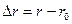, , , 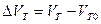фазовых координат r, V_R, V_T  от соответствующих значений r₀, , V_R=0,    на круговой орбите радиуса достаточно малы, линеаризуйте уравнения и приведите модель движения в отклонениях к виду

,

где , u = f_T. Начальное состояние по условию задачи – нулевой вектор.

Терминальное состояние определяется вектором 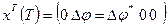, 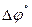- заданное угловое расстояние;

Т – длительность процесса перевода подлежит определению.

Оптимальное управление u(t) должно обеспечить выполнение терминальных условий и минимизировать критерий, характеризующий энергетические затраты

.

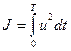Терминальные требования аппроксимировать квадратичным штрафом.

Примечание. В уравнениях движения целесообразно перейти к безразмерным переменным с использованием соотношений:

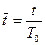, , , , где .