Параметрическая оптимизация управления спуском с орбиты

 

Летательный аппарат совершает посадку на планету с эллиптической орбиты в плоскопараллельном гравитационном поле. ЛА оснащен нерегулируемым маршевым двигателем.

В начальный момент времени ЛА находится в перицентре облетной орбиты. известны высота, скорость, масса конструкции и масса топлива на борту.

В момент касания поверхности планеты вертикальная и горизонтальная составляющие скорости должны быть в допустимых пределах.  

 

Модель движения

 

 

 

где h – высота;

       m – масса ЛА;

P – сила тяги двигателя;

J – удельный импульс;

β – секундный расход топлива;

β_m – максимально возможный расход топлива;

       g  – ускорение силы тяжести;

       g₀ – ускорение силы тяжести на поверхности планеты;

       R_P – радиус планеты. 

 

       Программа управления задана в параметрической форме  , где , ,  – неизвестные параметры.

Критерий оптимальности – расход топлива (максимум конечной массы).

Терминальные требования: Y(T)=Vx(T)=Vy(T)=0; X(T) – свободно.

 

Найти решение - параметры , ,  , при которых затраты топлива минимальны с учетом краевых условий.

Для решения использовать методы нулевого порядка.

Выбрать наиболее эффективный метод

 

Прототип и исходные данные – см Лунный модуль проекта Н1-Л3 (СССР)

 

Синтез системы стабилизации

 

Угловое движение ЛА относительно связанной оси Z (тангаж) с достаточной степенью точности можно представить уравнением моментов

 

,

,

 

где 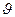 – угол тангажа;

α – угол атаки;

θ – угол наклона траектории;

δ – угол отклонения руля: ;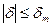

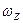– угловая скорость вращения вокруг оси Z;

– момент инерции;

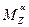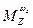, ,  – частные производные момента относительно оси Z по соответствующим переменным.

 

Упрощения: собственное демпфирование мало: .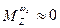

Угол наклона траектории изменяется очень медленно.

 

Найти закон управления углом δ, 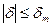 который обеспечит минимальное время регулирования при условиях .