Теорема. Если функция 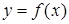 непрерывна на отрезке
непрерывна на отрезке  то на этом отрезке найдется такая точка
то на этом отрезке найдется такая точка 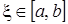 , что
, что
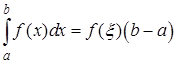 . (9)
. (9)
Доказательство. Пусть a<b и m и M – наименьшее и наибольшее значения функции на интервале, тогда в силу (8)
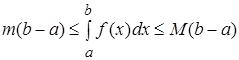
или

Обозначим  , причем
, причем  . Поскольку
. Поскольку 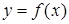 непрерывна, она принимает все значения, заключенные между m и M (теорема Коши о промежуточных значениях непрерывной функции). Следовательно, при некотором
непрерывна, она принимает все значения, заключенные между m и M (теорема Коши о промежуточных значениях непрерывной функции). Следовательно, при некотором 
 , т.е.
, т.е. 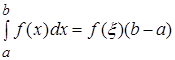 - что и требовалось доказать.
- что и требовалось доказать.
 Дадим наглядное геометрическое пояснение теоремы. Площадь криволинейной трапеции заключена между площадями прямоугольников
Дадим наглядное геометрическое пояснение теоремы. Площадь криволинейной трапеции заключена между площадями прямоугольников 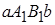 и
и  . Если прямая
. Если прямая  , параллельная оси 0x, смещается от положения
, параллельная оси 0x, смещается от положения  к положению
к положению  , то площадь
, то площадь  меняется непрерывно и в некотором положении окажется в точности равной площади криволинейной трапеции. При этом прямая
меняется непрерывно и в некотором положении окажется в точности равной площади криволинейной трапеции. При этом прямая  пересечет график функции в одной или нескольких точках Q с координатами
пересечет график функции в одной или нескольких точках Q с координатами 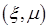 .
.
Число  – среднее значение функции
– среднее значение функции  на отрезке
на отрезке 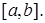
 2020-04-12
2020-04-12 159
159







