ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ПЛАН ЛЕКЦИИ
I. Определенный интеграл как предел интегральных сумм
II. Свойства определенного интеграла
III. Оценка интеграла
IV. Теорема о среднем. Среднее значение функции
I. Определенный интеграл как предел интегральных сумм. Рассмотрим геометрическую задачу о вычислении площади криволинейной трапеции - фигуры, ограниченной графиком непрерывной функции 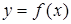 , прямыми
, прямыми 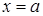 ,
, 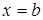 ,
, 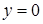 .
.
Предположим, что 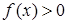 на отрезке
на отрезке 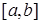 , то есть трапеция расположена над осью 0x. Разделим основание трапеции на n частичных интервалов
, то есть трапеция расположена над осью 0x. Разделим основание трапеции на n частичных интервалов 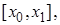
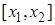 ,
, 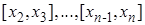 точками деления
точками деления 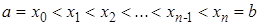 .
.
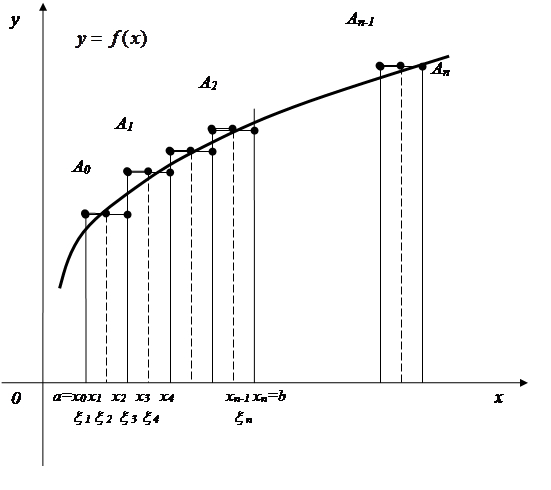 |
Проводя в точках деления прямые, параллельные оси 0y, разобьем рассматриваемую криволинейную трапецию
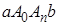 на n частичных трапеций:
на n частичных трапеций: 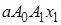 ,
, 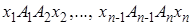 .. Возьмем в каждом из частичных интервалов произвольную точку
.. Возьмем в каждом из частичных интервалов произвольную точку 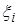 так, что
так, что 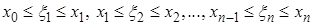 ..
..
В точках 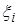 (i =1… n) проведем прямые, параллельные оси 0y, до пересечения с графиком функции
(i =1… n) проведем прямые, параллельные оси 0y, до пересечения с графиком функции 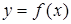 ; отрезки этих прямых соответственно равны
; отрезки этих прямых соответственно равны 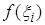 . На частичных интервалах построим n прямоугольников с высотами
. На частичных интервалах построим n прямоугольников с высотами 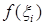 и получим n -ступенчатую фигуру, показанную на рисунке. Площадь Sn этой фигуры зависит от того, каким образом произведено разделение отрезка
и получим n -ступенчатую фигуру, показанную на рисунке. Площадь Sn этой фигуры зависит от того, каким образом произведено разделение отрезка 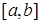 на интервалы, и от того, каким образом были выбраны точки
на интервалы, и от того, каким образом были выбраны точки 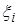 . Можно считать, что площадь Sn есть приближенное значение площади S криволинейной трапеции
. Можно считать, что площадь Sn есть приближенное значение площади S криволинейной трапеции 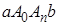 . Это приближение оказывается тем более точным, чем больше n и чем меньше длины частичных интервалов. Площадью криволинейной трапеции называют предел, к которому стремится площадь ступенчатой фигуры Sn при неограниченном возрастании n и стремлении к нулю наибольшей из длин частичных интервалов.
. Это приближение оказывается тем более точным, чем больше n и чем меньше длины частичных интервалов. Площадью криволинейной трапеции называют предел, к которому стремится площадь ступенчатой фигуры Sn при неограниченном возрастании n и стремлении к нулю наибольшей из длин частичных интервалов.
Если 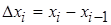 – длина i -ого конечного интервала, то условие
– длина i -ого конечного интервала, то условие 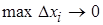 предполагает бесконечное измельчение отрезка
предполагает бесконечное измельчение отрезка 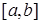 . Однако из того, что число точек деления
. Однако из того, что число точек деления 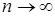 , не следует, что
, не следует, что 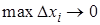 , поскольку точки деления xi могут быть выбраны произвольно. Если при измельчении отрезка
, поскольку точки деления xi могут быть выбраны произвольно. Если при измельчении отрезка 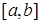 одна из точек, например
одна из точек, например 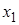 , фиксирована, то при этом длина отрезка
, фиксирована, то при этом длина отрезка 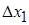 не стремится к нулю, хотя
не стремится к нулю, хотя 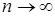 . При этом площадь рассматриваемой ступенчатой фигуры и в пределе не станет равной площади криволинейной трапеции.
. При этом площадь рассматриваемой ступенчатой фигуры и в пределе не станет равной площади криволинейной трапеции.
Запишем выражение для площади ступенчатой фигуры Sn как сумму площадей прямоугольников с основаниями 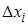 и высотами
и высотами 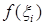 :
:
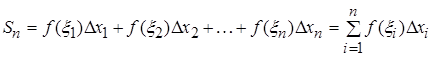 .
.
Тогда в соответствии с определением площади криволинейной трапеции
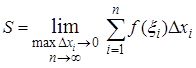 . (1)
. (1)
К пределам, аналогичным (1), приводят многие задачи физики и прикладных дисциплин (вычисление работы переменной силы, нахождение пройденного пути, вычисление массы и др.). Поэтому имеет смысл, отвлекаясь от физического смысла функции 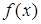 и переменной x, ввести соответствующее равенству (1) общее математическое понятие.
и переменной x, ввести соответствующее равенству (1) общее математическое понятие.
Определение. Если для функции 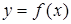 , непрерывной на отрезке
, непрерывной на отрезке 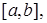 существует предел, к которому стремится n -ая интегральная сумма
существует предел, к которому стремится n -ая интегральная сумма 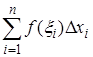 при стремлении к нулю длины наибольшего из частичных интервалов, и если этот предел не зависит ни от способа разбиения интервала интегрирования на частичные интервалы, ни от выбора в них промежуточных точек, то его называют определенным интегралом и обозначают
при стремлении к нулю длины наибольшего из частичных интервалов, и если этот предел не зависит ни от способа разбиения интервала интегрирования на частичные интервалы, ни от выбора в них промежуточных точек, то его называют определенным интегралом и обозначают
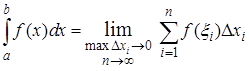 . (2)
. (2)
Как и в неопределенном интеграле, функцию 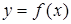 называют подынтегральной функцией,
называют подынтегральной функцией, 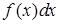 – подынтегральным выражением, x – переменной интегрирования, a – нижним и b – верхним пределами интегрирования.
– подынтегральным выражением, x – переменной интегрирования, a – нижним и b – верхним пределами интегрирования.
В отличие от неопределенного интеграла, представляющего собой семейство функций, определенный интеграл есть число. Величина его зависит только от вида подынтегральной функции и пределов a и b, определяющих интервал интегрирования, но не от переменной интегрирования, поэтому справедливы равенства
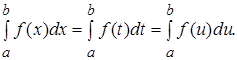
Если для функции 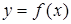 существует определенный интеграл
существует определенный интеграл  , то эта функция называется интегрируемой (по Риману) на отрезке [ a,b ].
, то эта функция называется интегрируемой (по Риману) на отрезке [ a,b ].
Отметим без доказательства, что
1) всякая непрерывная на отрезке 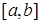 функция интегрируема на этом отрезке;
функция интегрируема на этом отрезке;
2) если ограниченная функция 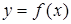 на отрезке
на отрезке 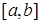 имеет лишь конечное число точек разрыва, то она интегрируема на этом отрезке;
имеет лишь конечное число точек разрыва, то она интегрируема на этом отрезке;
3) монотонная ограниченная функция всегда интегрируема.
II. Свойства определенного интеграла. К свойствам определенного интеграла относят следующие.
1. Свойство линейности, связанное с операциями над функциями: определенный интеграл над линейной комбинацией функций на отрезке равен линейной комбинации определенных интегралов от этих функций на том же отрезке:
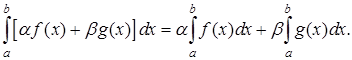 (3)
(3)
Доказательство. Воспользуемся определением интеграла для функции
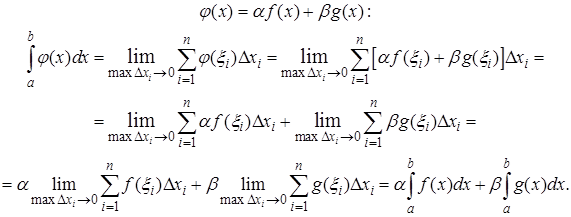
2. Свойства, связанные с отрезками интегрирования:
а) 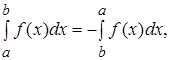 (4)
(4)
б) 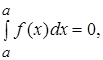 (5)
(5)
в) 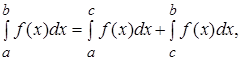 если
если 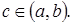 (6)
(6)
Доказательство. Поскольку для непрерывной функции предел интегральной суммы не зависит от способа разбиения, можно считать, что точка с совпадает с одной и той же точкой деления. При этом интегральную сумму можно представить в виде
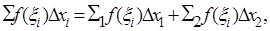 (7)
(7)
где в сумме Σ1 собраны все интервалы деления от a до c, в сумме Σ2 – от c до b и в сумме Σ – от a до b. Переходя в соотношении (7) к пределу, получим равенство, отражающее свойство (6), называемое аддитивностью определенного интеграла.
III. Оценка интеграла. Приведем некоторые теоремы, позволяющие проводить оценку определенного интеграла.
1. Если 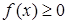 при всех
при всех 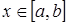 , то
, то 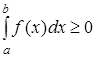 .
.
2. Если на отрезке 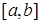 функции
функции 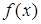 и
и 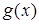 удовлетворяют условию
удовлетворяют условию 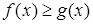 , то
, то 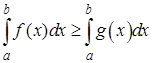 .
.
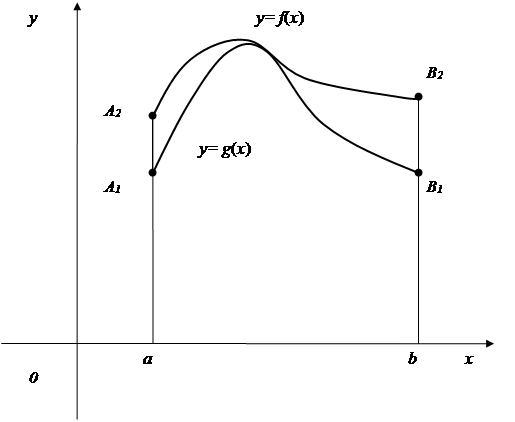
В случае, когда 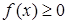 и
и 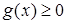 , последнее свойство имеет простую геометрическую иллюстрацию: площадь криволинейной трапеции
, последнее свойство имеет простую геометрическую иллюстрацию: площадь криволинейной трапеции 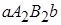 , ограниченной графиком функции
, ограниченной графиком функции 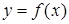 , больше площади криволинейной трапеции
, больше площади криволинейной трапеции 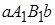 , ограниченной графиком функции
, ограниченной графиком функции 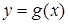 .
.
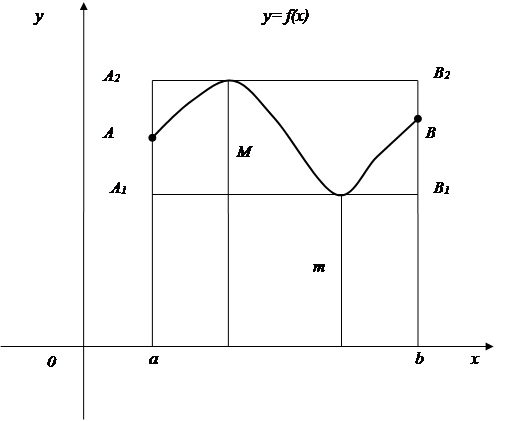
3. Если m и M – наименьшее и наибольшее значение функции 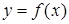 на отрезке [ a,b ], то
на отрезке [ a,b ], то
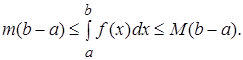 (8)
(8)
Доказательство. По условию 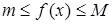
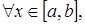 тогда
тогда
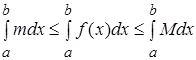
на основании предыдущего свойства.
 Но
Но 
и 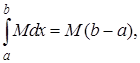
что при подстановке в последнее неравенство и приводит к соотношению (8).
Если 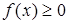 на отрезке [ a,b ], то неравенство (8) отражает тот факт, что площадь криволинейной трапеции
на отрезке [ a,b ], то неравенство (8) отражает тот факт, что площадь криволинейной трапеции 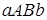 содержится между площадями прямоугольников
содержится между площадями прямоугольников 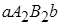 и
и 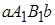 .
.
 2020-04-12
2020-04-12 251
251







