Математическое моделирование процессов управления

 

Математическое моделирование экономических явлений и процессов с целью оптимизации процессов управления - область научно-практической деятельности, получившая мощный стимул к развитию во время и сразу после второй мировой войны. Эта тематика развивалась в рамках интеллектуального движения, связанного с терминами "кибернетика", "исследование операций", а позже - "системный анализ", "информатика".

Особое место занимают имитационные системы, позволяющие отвечать на вопросы типа: "Что будет, если...?" Любая модель, в принципе, имитационная, ибо она имитирует реальность. Основа имитации - это математическая модель. Имитационная система - это совокупность моделей, имитирующих протекание изучаемого процесса, объединенная со специальной системой вспомогательных программ и информационной базой, позволяющих достаточно просто и оперативно реализовать вариантные расчеты. Таким образом, под имитацией понимается численный метод проведения машинных экспериментов с математическими моделями, описывающими поведение сложных систем в течение продолжительных периодов времени, при этом имитационный эксперимент, как правило, состоит из следующих этапов:

· формулировка задачи,

· построение математической модели,

· составление программы для ЭВМ,

· оценка пригодности модели,

· планирование эксперимента,

· обработка результатов эксперимента.

Имитационное моделирование (simulation modelling) широко применяется в различных областях, в том числе в экономике.

Экономико-математические методы управления можно разделить на несколько групп:

- методы оптимизации,

- методы, учитывающие неопределенность, прежде всего вероятностно-статистические,

- методы построения и анализа имитационных моделей,

- методы анализа конфликтных ситуаций (теории игр).

 

Основные термины математического моделирования.

 

В качестве основных терминов, относящихся к разделу математического моделирования, можно предложить:

- компоненты системы - части системы, которые могут быть вычленены из нее и рассмотрены отдельно;

- независимые переменные – они могут изменяться, но это внешние величины, не зависящие от проходящих в системе процессов;

- зависимые переменные - значения этих переменных есть результат (функция) воздействия на систему независимых внешних переменных;

- управляемые (управляющие) переменные - те, значения которых могут изменяться исследователем;

- внутренние переменные – их значения определяются в ходе деятельности компонент системы (т.е. “внутри” системы);

- внешние переменные - определяются либо исследователем, либо извне, т.е. в любом случае действуют на систему извне.

При построении любой модели процесса управления желательно придерживаться следующего плана действий:

· Сформулировать цели изучения системы;

· Выбрать те факторы, компоненты и переменные, которые являются наиболее существенными для данной задачи;

· Учесть тем или иным способом посторонние, не включенные в модель факторы;

· Осуществить оценку результатов, проверку модели, оценку полноты модели.

Для моделирования ситуации вначале нужно представить ее структурированным образом, т.е. необходимо выработать некий способ, который позволит привести ситуацию в упорядоченный вид. Постановка проблемывключает в себя возможные решения и метод измерения их эффективности. Структурирование — это навык переходить от признака к четкой постановке проблемы.

При количественном моделировании бизнес-среды необходимо описывать взаимодействия многих переменных. Для этого нужно сформулировать математическую модель. В реальном мире обычно не существует единственно верного способа построения модели. Различные модели могут дать различные представления об одной и той же ситуации.

  Общие сведения об оптимизации Термин «оптимальный» произошел от латинского «optimus», что означает наилучший, совершенный. Классическая математика связывает нахождение оптимума с нахождением максимума или минимума некоторой функции, определяющей зависимость критерия оптимальности от некоторых аргументов (факторов) процесса, явления или системы. Сама цепочка процедур по отысканию наилучшего решения (глобального экстремума) называется оптимизацией. Прикладные задачи часто содержат различные ограничения в виде равенств и неравенств, специфические функции и не могут быть решены только классическими методами. Для решения таких задач весьма эффективны численные методы, получившие в наши дни второе дыхание в связи с бурным развитием компьютерной техники. Методы оптимизации эффективно применяются в самых различных областях человеческой деятельности. Но самые значительные успехи достигнуты при анализе и проектировании сложных технических объектов (космические комплексы, атомные электростанции, летательные аппараты и т.д.). В сельском хозяйстве машины нового поколения представляют собой сложнейшую совокупность различных мехатронных систем. Речь идет о современных посевных комплексах, доильных установках, зерноуборочных комбайнах, линиях по переработке сельскохозяйственной продукции и т.д. Очевидно, что без компьютерного анализа и оптимизации современные машины, конкурирующие с зарубежными, создать невозможно. Сложные задачи в большинстве своем многокритериальные, и с улучшением одних критериев, другие ухудшаются. Речь идет о таких противоречивых критериях как материалоемкость, энергоемкость, производительность, прочность, долговечность, коэффициент полезного действия, габариты, показатели качества работы, эргономичность и т.д. Свести многокритериальные задачи к однокритериальным чаще всего не удается. Тогда приходится решать компромиссную задачу, при этом необходимо учесть множество ограничений и требований. Такие задачи обычно осложняются размытым характером действующих факторов. В этом случае классические методы оптимизации чаще всего бессильны. Чем сложнее система, тем меньше вероятность найти для нее строго оптимальное решение. Поэтому необходимо применять методы принятия решений. Эти методы составляют относительно новую науку – теорию принятия решений, пересекающуюся с такими дисциплинами, как системный анализ, исследование операций, теория игр и т.д. Следует отметить, что современная теория принятия решений имеет обширный инструментарий в виде развитого математического аппарата и современных вычислительных алгоритмов. Эвристические приемы, включающие опыт и интуицию, способности человека к ассоциациям и многое другое, что лежит вне математики, играют в этой теории большую, а иногда и решающую роль. Вспомним успешные шахматные баталии наших чемпионов с суперкомпьютерами. Как человек может победить в шахматы машину, которая совершает миллиарды операций в секунду и анализирует миллионы вариантов шахматных ходов? Именно за счет включения свойств человеческого ума, которые были перечислены выше. В инженерных многокритериальных задачах дело математики выдать не окончательное решение, а помочь специалисту проанализировать отдельные варианты, показать, к каким последствиям приведет их осуществление и т.д. Проектировщики, конструкторы постоянно решают подобные многокритериальные задачи с взаимоисключающими требованиями. При проектировании простой детали уже возникает проблема минимизации веса и в то же время обеспечения требуемой ее прочности. Чтобы расход горючего трактора и его пагубное воздействие на почву были минимальными, он должен быть легок, однако требование увеличения тягового усилия требует его утяжеления. В инженерно-технической сфере сельского хозяйства постоянно возникают оптимизационные задачи, требующие неформального участия специалиста. К таким задачам относятся: - оптимизация состава машинно-тракторного парка; - оптимизация распределения работ и услуг технического сервиса между исполнителями работ; - выбор оптимального набора машин для механизации технологических процессов в животноводстве и переработке сельскохозяйственной продукции; - оптимальная реконструкция электрических распределительных систем и т.д. При этом также приходится вводить антагонистичные критерии оптимальности, например, число исполнителей и время обслуживания машинно-тракторного парка. Решению задачи оптимизации в реальной производственной, проектной или научной проблеме предшествует ряд предварительных процедур: 1) словесное или содержательное описание инженерной задачи и ее целевого назначения; 2) выбор критерия (или критериев) оптимальности, управляемых переменных (факторов), введение обозначений; 3) введение ограничений и допущений; 4) разработка математической модели в принятых обозначениях и терминах.

Собственно оптимизация включает два этапа: 1) выбор методов и алгоритмов решения оптимизационной задачи, ее реализация в аналитическом или численном виде; 2) анализ полученных результатов, их интерпретация и принятие решения. В инженерной деятельности при оптимизации приходится иметь дело с техническими системами, машинами, аппаратами, устройствами, технологическими процессами и т.д. При решении задач оптимизации всю их совокупность будем называть объектами оптимизации. Одной из первых и основных проблем в оптимизационной задаче является выбор критерия оптимальности, т.е. основного признака, на основании которого проводится сравнительная оценка возможных решений (альтернатив) и выбор наилучшего. В качестве синонимов критерия оптимальности в технической литературе можно встретить такие термины как показатель оптимальности, критерий эффективности, критерий поиска, параметр оптимальности, функция цели (целевая функция), выход модели, выходной параметр и т.д. Выбор критерия оптимальности, недостаточно полно отражающего суть инженерной задачи, может привести к серьезным просчетам и не достижению цели оптимизации. Кстати, цель оптимизации не всегда может совпадать с критерием оптимальности. Например, об однородности кормовой смеси (цель оптимизации) судят по равномерности распределения в смеси контрольного компонента (критерий оптимальности). Критерием оптимальности мы можем выбрать скорость машинно-тракторного агрегата, хотя целью оптимизации является достижение максимальной производительности. Целевая функция содержит ряд параметров оптимизации (факторов), с помощью которых мы можем изменить значение критерия оптимальности. Эти параметры можно разделить на внутренние и внешние. Если речь идет о технологическом процессе сельскохозяйственного назначения, то внутренними следует считать следующие параметры: 1) геометрические параметры (диаметр, длина рабочего органа, зазор, высота слоя материала и т.д.); 2) кинематические параметры рабочего органа (угловая скорость, линейная скорость, частота и амплитуда вибрации и т.д.); 3) технологические свойства перерабатываемого сырья (коэффициент трения, модуль упругости, размерные характеристики, скорости витания, сопротивление почвы и т.д.). Внешние параметры характеризуют влияние внешней среды (температура, влажность, направление ветра и т.д.). При проектировании иногда оптимизируется структура технического объекта. К примеру, при создании гибридного автомобиля решаются вопросы использования, взаимодействия и расположения двигателя внутреннего сгорания, генератора, электродвигателей и аккумуляторов. В связи со сказанным, оптимизацию конструкции технического устройства или технологического процесса можно разделить на следующие виды: 1) структурную, когда оптимизируется схема и принцип действия технического средства или технологического процесса; 2) параметрическую, когда отрабатываются параметры технического объекта или процесса. В реальных технических задачах существует ряд ограничений, обусловленных физической реализуемостью процесса, требованиями стандартов, регламентов, ограничениями на ресурсы, экономическими, экологическими требованиями и т.д. Поэтому оптимизацию в прикладных задачах можно характеризовать как процесс нахождения наилучшего решения при заданных условиях, ограничениях и критериях. С учетом сказанного, в самом общем виде задачу оптимизации при одном критерии оптимальности можно записать следующим образом: f(x1,x2,…,xn)→max(min), (x1,x2,…,xn) ∊ D, (1) где f (x1, x2,…, xn) - целевая функция; x1, x2,…, xn - параметры оптимизации; D - область допустимых решений. Точку x* в пространстве с координатами (x1*, x2*,…, xn*)∊ D, в которой целевая функция достигает нужного нам наибольшего или наименьшего значения, называют оптимальным решением. Например, мы говорим «оптимальная скорость легкового автомобиля», подразумевая под этим, например, минимум расхода бензина на 100 км пути, как критерий оптимальности.

Краткая характеристика методов оптимизации При решении конкретной задачи оптимизации исследователь или конструктор прежде всего должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. Выбор того или иного метода в значительной степени определяется постановкой оптимальной задачи, а также используемой математической моделью объекта оптимизации. В настоящее время для решения оптимальных задач применяют в основном следующие методы:

- методы исследования функций классического анализа;

- методы, основанные на использовании неопределенных множителей Лагранжа;

- вариационное исчисление;

- динамическое программирование;

- принцип максимума;

- линейное программирование;

- нелинейное программирование.·

В последнее время разработан и успешно применяется для решения определенного класса задач метод геометрического программирования.

Как правило, нельзя рекомендовать какой-либо один метод, который можно использовать для решения всех без исключения задач, возникающих на практике. Одни методы в этом отношении являются более общими, другие - менее общими. Наконец, целую группу методов (методы исследования функций классического анализа, метод множителей Лагранжа, методы нелинейного программирования) на определенных этапах решения оптимальной задачи можно применять в сочетании с другими методами, например динамическим программированием или принципом максимума. Отметим также, что некоторые методы специально разработаны или наилучшим образом подходят для решения оптимальных задач с математическими моделями определенного вида. Так, математический аппарат линейного программирования, специально создан для решения задач с линейными критериями оптимальности и линейными ограничениями на переменные и позволяет решать большинство задач, сформулированных в такой постановке. Так же и геометрическое программирование предназначено для решения оптимальных задач, в которых критерий оптимальности и ограничения представляются специального вида функциями - позиномами. Динамическое программирование хорошо приспособлено для решения задач оптимизации многостадийных процессов, особенно тех, в которых состояние каждой стадии характеризуется относительно небольшим числом переменных состояния. Однако при наличии значительного числа этих переменных, т. е. при высокой размерности каждой стадии, применение метода динамического программирования затруднительно вследствие ограниченных быстродействия и объема памяти вычислительных машин. Пожалуй, наилучшим путем при выборе метода оптимизации, наиболее пригодного для решения соответствующей задачи, следует признать исследование возможностей и опыта применения различных методов оптимизации.

Краткий обзор математических методов решения оптимальных задач и областей их применения, что до некоторой степени может облегчить выбор того или иного метода для решения конкретной оптимальной задачи.

  Методы исследования функций классического анализа представляют собой наиболее известные методы решения несложных оптимальных задач, которые излагаются в курсе математического анализа. Обычной областью использования данных методов являются задачи с известным аналитическим выражением критерия оптимальности, что позволяет найти не очень сложное, также аналитическое выражение для производных. Полученные приравниванием нулю производных уравнения, определяющие экстремальные решения оптимальной задачи, крайне редко удается решить аналитическим путем, поэтому, как, правило, применяют вычислительные машины. При этом надо решить систему конечных уравнений, чаще всего нелинейных, для чего приходится использовать численные методы, аналогичные методам нелинейного программирования. Дополнительные трудности при решении оптимальной задачи методами исследования функций классического анализа возникают вследствие того, что система уравнений, получаемая в результате их применения, обеспечивает лишь необходимые условия оптимальности. Поэтому все решения данной системы (а их может быть и несколько) должны быть проверены на достаточность. В результате такой проверки сначала отбрасывают решения, которые не определяют экстремальные значения критерия оптимальности, а затем среди остающихся экстремальных решений выбирают решение, удовлетворяющее условиям оптимальной задачи, т. е. наибольшему или наименьшему значению критерия оптимальности в зависимости от постановки задачи. Методы исследования при наличии ограничений на область изменения независимых переменных можно использовать только для отыскания экстремальных значений внутри указанной области. В особенности это относится к задачам с большим числом независимых переменных (практически больше двух), в которых анализ значений критерия оптимальности на границе допустимой области изменения переменных становится весьма сложным.

Метод множителей Лагранжа применяют для решения задач такого же класса сложности, как и при использовании обычных методов исследования функций, но при наличии ограничений типа равенств на независимые переменные. К требованию возможности получения аналитических выражений для производных от критерия оптимальности при этом добавляется аналогичное требование относительно аналитического вида уравнений ограничений. В основном при использовании метода множителей Лагранжа приходится решать те же задачи, что и без ограничений. Некоторое усложнение в данном случае возникает лишь от введения дополнительных неопределенных множителей, вследствие чего порядок системы уравнений, решаемой для нахождения экстремумов критерия оптимальности, соответственно повышается на число ограничений. В остальном, процедура поиска решений и проверки их на оптимальность отвечает процедуре решения задач без ограничений. Множители Лагранжа можно применять для решения задач оптимизации объектов на основе уравнений с частными производными и задач динамической оптимизации. При этом вместо решения системы конечных уравнений для отыскания оптимума необходимо интегрировать систему дифференциальных уравнений. Следует отметить, что множители Лагранжа используют также в качестве вспомогательного средства и при решении специальными методами задач других классов с ограничениями типа равенств, например, в вариационном исчислении и динамическом программировании. Особенно эффективно применение множителей Лагранжа в методе динамического программирования, где с их помощью иногда удается снизить размерность решаемой задачи.

Методы вариационного исчисления обычно используют для решения задач, в которых критерии оптимальности представляются в виде функционалов и решениями которых служат неизвестные функции. Такие задачи возникают обычно при статической оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации. Вариационные методы позволяют в этом случае свести решение оптимальной задачи к интегрированию системы дифференциальных уравнений Эйлера, каждое из которых является нелинейным дифференциальным уравнением второго порядка с граничными условиями, заданными на обоих концах интервала интегрирования. Число уравнений указанной системы при этом равно числу неизвестных функций, определяемых при решении оптимальной задачи. Каждую функцию находят в результате интегрирования получаемой системы. Уравнения Эйлера выводятся как необходимые условия экстремума функционала. Поэтому полученные интегрированием системы дифференциальных уравнений функции должны быть проверены на экстремум функционала. При наличии ограничений типа равенств, имеющих вид функционалов, применяют множители Лагранжа, что дает возможность перейти от условной задачи к безусловной. Наиболее значительные трудности при использовании вариационных методов возникают в случае решения задач с ограничениями типа неравенств. Заслуживают внимания прямые методы решения задач оптимизации функционалов, обычно позволяющие свести исходную вариационную задачу к задаче нелинейного программирования, решить которую иногда проще, чем краевую задачу для уравнений Эйлера.

Динамическое программирование служит эффективным методом решения задач оптимизации дискретных многостадийных процессов, для которых критерий оптимальности задается как аддитивная функция критериев оптимальности отдельных стадий. Без особых затруднений указанный метод можно распространить и на случай, когда критерий оптимальности задан в другой форме, однако при этом обычно увеличивается размерность отдельных стадий. По существу метод динамического программирования представляет собой алгоритм определения оптимальной стратегии управления на всех стадиях процесса. При этом закон управления на каждой стадии находят путем решения частных задач оптимизации последовательно для всех стадий процесса с помощью методов исследования функций классического анализа или методов нелинейного программирования. Результаты решения обычно не могут быть выражены в аналитической форме, а получаются в виде таблиц. Ограничения на переменные задачи не оказывают влияния на общий алгоритм решения, а учитываются при решении частных задач оптимизации на каждой стадии процесса. При наличии ограничений типа равенств иногда даже удается снизить размерность этих частных задач за счет использования множителей Лагранжа. Применение метода динамического программирования для оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации приводит к решению дифференциальных уравнений в частных производных. Вместо решения таких уравнений зачастую значительно проще представить непрерывный процесс как дискретный с достаточно большим числом стадий. Подобный прием оправдан особенно в тех случаях, когда имеются ограничения на переменные задачи и прямое решение дифференциальных уравнений осложняется необходимостью учета указанных ограничений. При решении задач методом динамического программирования, как правило, используют вычислительные машины, обладающие достаточным объемом памяти для хранения промежуточных результатов решения, которые обычно получаются в табличной форме.

Принцип максимума применяют для решения задач оптимизации процессов, описываемых системами дифференциальных уравнений. Достоинством математического аппарата принципа максимума является то, что решение может определяться в виде разрывных функций; это свойственно многим задачам оптимизации, например задачам оптимального управления объектами, описываемыми линейными дифференциальными уравнениями. Нахождение оптимального решения при использовании принципа максимума сводится к задаче интегрирования системы дифференциальных уравнений процесса и сопряженной системы для вспомогательных функций при граничных условиях, заданных на обоих концах интервала интегрирования, т. е. к решению краевой задачи. На область изменения переменных могут быть наложены ограничения. Систему дифференциальных уравнений интегрируют, применяя обычные программы на вычислительных машинах. Принцип максимума для процессов, описываемых дифференциальными уравнениями, при некоторых предположениях является достаточным условием оптимальности. Поэтому дополнительной проверки на оптимум получаемых решений обычно не требуется. Для дискретных процессов принцип максимума в той же формулировке, что и для непрерывных, вообще говоря, несправедлив. Однако условия оптимальности, получаемые при его применении для многостадийных процессов, позволяют найти достаточно удобные алгоритмы оптимизации.

Методы нелинейного программирования применяют для решения оптимальных задач с нелинейными функциями цели. На независимые переменные могут быть наложены ограничения также в виде нелинейных соотношений, имеющих вид равенств или неравенств. По существу методы нелинейного программирования используют, если ни один из перечисленных выше методов не позволяет сколько-нибудь продвинуться в решении оптимальной задачи. Поэтому указанные методы иногда называют также прямыми методами решения оптимальных задач. Названием “методы нелинейного программирования” объединяется большая группа численных методов, многие из которых приспособлены для решения оптимальных задач соответствующего класса. Выбор того или иного метода обусловлен сложностью вычисления критерия оптимальности и сложностью ограничивающих условий, необходимой точностью решения, мощностью имеющейся вычислительной машины и т.д. Ряд методов нелинейного программирования практически постоянно используется в сочетании с другими методами оптимизации, как, например, метод сканирования в динамическом программировании. Кроме того, эти методы служат основой построения систем автоматической оптимизации - оптимизаторов, непосредственно применяющихся для управления производственными процессами.

Геометрическое программирование есть метод решения одного специального класса задач нелинейного программирования, в которых критерий оптимальности и ограничения задаются в виде позиномов - выражений, представляющих собой сумму произведений степенных функций от независимых переменных. С подобными задачами иногда приходится сталкиваться в проектировании. Кроме того, некоторые задачи нелинейного программирования иногда можно свести к указанному представлению, используя аппроксимацию целевых функций и ограничений. Важной характеристикой любой оптимальной задачи является ее размерность п, равная числу переменных, задание значений которых необходимо для однозначного определения состояния оптимизируемого объекта. Как правило, решение задач высокой размерности связано с необходимостью выполнения большого объема вычислений. Ряд методов (например, динамическое программирование и дискретный принцип максимума) специально предназначен для решения задач оптимизации процессов высокой размерности, которые могут быть представлены как многостадийные процессы с относительно невысокой размерностью каждой стадии.

Линейное программирование представляет собой математический аппарат, разработанный для решения оптимальных задач с линейными выражениями для критерия оптимальности и линейными ограничениями на область изменения переменных. Такие задачи обычно встречаются при решении вопросов оптимального планирования производства с ограниченным количеством ресурсов, при определении оптимального плана перевозок (транспортные задачи) и т.д. Для решения большого круга задач линейного программирования имеется практически универсальный алгоритм - симплексный метод, позволяющий за конечное число итераций находить оптимальное решение подавляющего большинства задач. Тип используемых ограничений (равенства или неравенства) не сказывается на возможности применения указанного алгоритма. Дополнительной проверки на оптимальность для получаемых решений не требуется. Как правило, практические задачи линейного программирования отличаются весьма значительным числом независимых переменных. Поэтому для их решения обычно используют вычислительные машины, необходимая мощность которых определяется размерностью решаемой задачи.

Среди задач экономики и управления производством наиболее известны задачи оптимального планирования, к которым относится достаточно широкий круг задач оптимизации.

Задача оптимизации – это задача выбора таких условий и зависящих от них факторов, при которых критерий эффективности достигает экстремального значения.

Под решением задач оптимизации понимается процесс выбора таких значений переменных х, принадлежащих допустимой области D, которые обеспечивают оптимальное значение некоторой функции F(x), называемой целевой.

Если целевая функция линейна, а область допустимых значений задается системой линейных уравнений или неравенств, то такая задача является задачей линейного программирования.

Модель задачи линейного программирования должна иметь вполне определенный вид: требуется найти максимум (минимум) значения целевой функции L при переменных x₁, x_2…, x_n

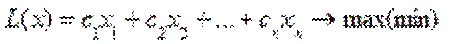(1)

при соблюдении линейных ограничений

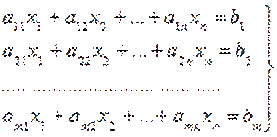(2)

Каждая из переменных не может принимать отрицательного значения, то есть

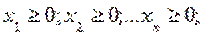(3)

В выражениях (1) и (2) коэффициенты a_ij и c_j при переменных и величины b_i - постоянные числа.

Допустимое решение – это совокупность чисел (план) 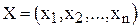, удовлетворяющих ограничениям задачи.

Оптимальное решение – это план, при котором целевая функция (ЦФ) принимает свое максимальное (минимальное) значение.

Решение задачи линейного программирования называется вырожденным, если в нём некоторые переменные равны нулю. В противном случае решение является невырожденным.

Рассмотрим пример построения математической модели задачи и порядок её решения в среде табличного процессора MS Excel.

Условие задачи: В хозяйстве имеется 200 га неиспользуемых земель, пригодных для освоения под пашню и сенокос. Затраты труда на освоение 1 га земель под пашню составляют 37 чел.-ч., в сенокос 1 чел.-ч. Для вовлечения земель в сельскохозяйственный оборот предприятие может затратить не более 1200 чел.-ч. механизированного труда. Стоимость продукции, получаемой с 1 га пашни, составляет 16000 руб., с 1 га сенокосов -2000 руб. В задание на проектирование установлено, что площадь земель осваиваемых под пашню не должна превышать 50 % площади сенокосов. Требуется определить, какую площадь нужно освоить под пашню и сенокосы, чтобы получить максимальное количество продукции в стоимостном выражении.

1. Построим математическую модель задачи

1.1Введем переменные

Х1 - площадь земель трансформируемая в пашню, га,

Х2 - площадь земель трансформируемая в сенокосы, га.

1.2Запишем ограничения

1) По площади неиспользуемых земель, пригодных для освоения под пашню и сенокосы, га

Х1 + Х2 ≤ 200

2) По затратам труда, чел - ч.

37Х1 +Х2 ≤ 1200

3) По соотношению площадей земель осваиваемых под пашню и под сенокосы, га

Х1 ≤ 0,5Х2

1.3Наложим условие неотрицательности на переменные

Х1≥ 0, Х2≥0.

1.4Запишем целевую функцию (критерий оптимальности - максимальный выход продукции, рублей)

Z= 16000Х1 +2000Х2 → max

Сформулируем математическую задачу: найти такие значения переменных Х1 и Х2, чтоб выполнялись ограничения задачи и достигалось максимальное значение целевой функции Z.

2 Построим матрицу модели

Таблица 1 Матрица модели

Ограничения	Площадь под пашню, га, Х1	Площадь под сенокосы, га, Х2	Тип ограничения	Объем ограничения
1. 1. Общая площадь, га 2.Трудовые ресурсы, чел.-ч 3.Соотношение площадей, га 4.ЦФ(max выход продукции)	1   37   1   16000	1   1   -0,5   2000	<=   <=   <=   =>	200   1200   0   max

Сформулируем экономическую задачу: найти площадь земли, трансформируемую под пашню и площадь земли, трансформируемую в сенокосы, чтобы уложиться в выделенные ресурсы земли и труда, а также выполнить задание на проектирование по соотношению площадей земель осваиваемых под пашню и под сенокосы. При этом получить максимальное количество продукции в стоимостном выражении.

Затем решается задача в Excel с помощью надстройки Поиск решения, которая позволяет решать оптимизационные задачи.

Последовательность решения задачи

1) Создать форму для ввода условий задачи.

2) Ввести исходные данные.

3) Ввести зависимость для целевой функции.

4) Ввести зависимости для ограничений.

Запуск на решение задачи

1) Запустить Поиск решения.

2) Указать назначение целевой функции (установить целевую ячейку).

3) Установить изменяемые ячейки.

4) Ввести ограничения.

5) Ввести параметры для решения задачи линейного программирования (ЗЛП).