2020-04-12
110
Задание 4. Найти линейную комбинацию матриц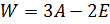 
.
Решение. Линейные операции над матрицами производятся покоординатно и выглядят абсолютно аналогично соответствующим операциям над векторами:
W <- 3*A-2*E # Арифметические операции над матрицами, сохраненные в матрице W
W # Можно вывести на экран результат W
> W <- 3*A-2*E # Арифметические операции над матрицами, сохраненные в матрице W> W # Можно вывести на экран результат W [,1] [,2] [,3][1,] 1 6 9[2,] 12 13 18[3,] 21 24 25Здесь важно помнить, что размерности слагаемых должны быть одинаковыми. Так, например, невозможно сложить матрицы разных размерностей
:
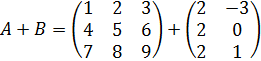A+B # Попытка сложить матрицы разных размерностей
что немедленно приводит к сообщению об ошибке:
> A+B # Попытка сложить матрицы разных размерностейError in A + B: non-conformable arraysПроизведение матриц
Задание 5. Найти матричные значения указанных выражений
a)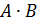 
b)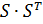 
c)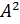 
d)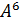 
e)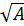 
Решение. Матричное произведение в R отличается от покоординатного произведения и оформляется в специальных «процентных» скобках: %*%
A %*% B # Произведение матриц A и B
S %*% t(S) # Произведение матриц S и t(S)
A %*% A # Матричный квадрат матрицы A²
с результатом в консоли
> A %*% B # Произведение матриц A и B
[,1] [,2]
[1,] 12 0
[2,] 30 -6
[3,] 48 -12
> S %*% t(S) # Произведение матриц S и t(S)
[,1] [,2] [,3]
[1,] 43 -20 64
[2,] -20 65 -14
[3,] 64 -14 367
> A %*% A # Матричный квадрат матрицы A²
[,1] [,2] [,3]
[1,] 30 36 42
[2,] 66 81 96
[3,] 102 126 150
Кстати, в первом случае произведение матриц в обратном порядке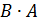 
не существует из-за несоответствия размерностей. Напомним, что для матричного произведения необходимо, чтобы количество столбцов в первой матрице было равно количеству строк второй матрицы.
В третьем случае ошибкой было бы записать A^2, т.к. эту форму компилятор R воспринимает как покоординатное произведение элементов и представляет результат как A*A. Запустите следующий ниже код и посмотрите разницу между покоординатным квадратом A*A=A^2 и матричным возведением в степень A%*%A:
A*A # Поэлементные квадраты чисел в матрице A. Можно и так: A^2
A%*%A # Квадрат матрицы A (сравните с предыдущим результатом!)
Возведение в степень
Для вычисления старших степеней матрицы удобно использовать специальную библиотеку expm. Напомним, что при самом первом использовании какой-либо библиотеки на используемом компьютере необходимо выполнить первоначальную загрузку пакета из интернета командой install.packages("Имя пакета") или использовать меню Rstudio: Tools -> install packages.
library(expm) # Активация библиотеки expm
A%^%5 # Пятая степень матрицы A
sqrtm(A) # Корень из матрицы A
> A%^%5 # Пятая степень матрицы A
[,1] [,2] [,3]
[1,] 121824 149688 177552
[2,] 275886 338985 402084
[3,] 429948 528282 626616
> sqrtm(A) # Корень из матрицы A
[,1] [,2] [,3]
[1,] 0.4497564+0.7622786i 0.5526217+0.2067958i 0.6554871-0.3486869i
[2,] 1.0185207+0.0841514i 1.2514702+0.0228291i 1.4844197-0.0384931i
[3,] 1.5872851-0.5939759i 1.9503187-0.1611376i 2.3133523+0.2717007i
В последнем примере с матричным корнем sqrtm(A) результатом является одна из матриц, квадрат которой совпадает с матрицей A. Легко заметить, что полученный результат – комплекснозначная матрица.
Проверим результат вычисления одного из корней матрицы sqrtm(A):
sqrtm(A)%*%sqrtm(A) # Возведем в квадрат матрицу sqrtm(A)
и получим исходную матрицу A:
> sqrtm(A)%*%sqrtm(A)
[,1] [,2] [,3]
[1,] 1+0i 2+0i 3-0i
[2,] 4+0i 5-0i 6+0i
[3,] 7+0i 8+0i 9+0i
Определители матриц
Задание 6. Для матрицы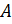 
найти
a) Элемент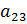 
b)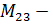 
минор элемента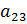
c)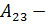 
алгебраическое дополнение 
элемента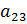
d) Определитель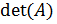 
матрицы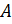
Решение. Отработайте поочередно каждую строчку кода и проверьте совпадают ли ответы с теоретическими:
A # Матрица A
> A # Матрица A [,1] [,2] [,3][1,] 1 2 3[2,] 4 5 6[3,] 7 8 9
A[2, 3] # Элемент a23 матрицы A
> A[2, 3] # Элемент a23 матрицы A[1] 6
A[-2,-3] # Матрица A без 2-ой строки и 3-его столбца
> A[-2,-3] # Матрица A без 2-ой строки и 3-его столбца [,1] [,2][1,] 1 2[2,] 7 8
det(A[-2,-3]) # Минор к элементу a23 матрицы A
> det(A[-2,-3]) # Минор к элементу a23 матрицы A[1] -6
(-1)^(2+3)*det(A[-2,-3]) # Алгебраическое дополнение к элементу a23 матрицы A
> (-1)^(2+3)*det(A[-2,-3]) # Алгебраическое дополнение к элементу a23 матрицы A[1] 6
det(A) # Определитель A (в теории точный ноль!)
> det(A) # Определитель A (в теории точный ноль!)[1] -9.517127e-16Здесь необходимо дать некоторые пояснения. Функция численного нахождения определителя матрицы det(A) реализует метод Гаусса – самый быстрый из существующих для больших размерностей матриц. Однако, для целочисленных матриц результат может оказаться числом не целым.
Ниже мы приводим код пользовательской функции Det(A) – разложения определителя по первой строке, которая для целочисленых матриц вычисляет точное значение определителя Данное задание выполняется по желанию студента:
Det <- function(A) {
n <- nrow(A); m <- ncol(A)
if (n!= m) {return("Матрица не квадратная!")} else {
if (n==1) {Rez <- A[1, 1]} else {
Rez <- 0
for (j in 1:n) {
B <- as.matrix(A[-1, -j])
Rez <- Rez + (-1)^(1+j)*A[1, j]*Det(B)
}
}
return(Rez)
}
}
# Пример использования
A <- matrix(1:9, 3, 3, byrow = TRUE)
A
Det(A) # Разложение определителя по 1-ой строке
det(A) # Метод Гаусса (встроенная в R функция)
Следует все же отметить, что для матриц больших размерностей (более 10 x 10) точный алгоритм Det(A) заметно уступает по скорости приближенному det(A).
Обратная матрица
Задание 7. Найти обратную матрицу к матрице
a)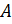
b)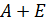 
Решение. Обратная матрица в R вызывается базовой функцией solve(…), которая возвращает требуемый результат для любой невырожденной матрицы (det(A)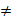 
0):
solve(A) # Обратная матрица к A не существует, т.к. det(A)=0 (см. выше)
solve(A+E) # Обратная матрица к A+E
с результатом:
> solve(A) # Обратная матрица к A не существует, т.к. det(A)=0 (см. выше)
Error in solve.default(A):
system is computationally singular: reciprocal condition number = 3.7011e-18
> solve(A+E) # Обратная матрица к A+E
[,1] [,2] [,3]
[1,] -6 -2.0 3.000000e+00
[2,] -1 0.5 2.219904e-17
[3,] 5 1.0 -2.000000e+00
Проверьте, все ли корректно: матрично перемножьте (A+E) и solve(A+E), в результате чего должна получиться единичная матрица (или ее «машинный» аналог).
Ранг матрицы
Задание 8. Найти обратную матрицу к матрице
a)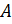
b)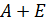
Решение. Для нахождения ранга матрицы потребуется специализированная библиотека Matrix, также требующая первоначальной установки:
library(Matrix) # Активация библиотеки Matrix
rankMatrix(A)[1] # Ранг матрицы A
rankMatrix(A+E)[1] # Ранг матрицы A+E
> library(Matrix) # Активация библиотеки Matrix
> rankMatrix(A)[1] # Ранг матрицы A
[1] 2
> rankMatrix(A+E)[1] # Ранг матрицы A+E
[1] 3
Вместо заключения
Напомним, что любой результат из R можно вернуть обратно в Excel в виде объекта X (X – число, вектор, матрица) следующей строкой кода:
# Скопировать в буфер обмена объект X в excel-формате:
write.table(X,"clipboard",quote=FALSE, col.names = FALSE, row.names = FALSE, sep = "\t",dec=",") # Не забыть выгрузить результат в Excel из буфера командой Ctrl + v
