Аналитически
Для вычисления данного интеграла используем формулу интегрирования по частям:
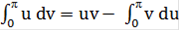 .
.
Пусть:
u = x
dv = cos (x) dx
Тогда:
du = dx
v = sin(x)
Следовательно:
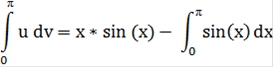
Откуда получаем:
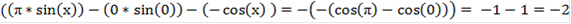
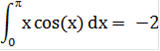
Метод средних прямоугольников
Метод прямоугольников получается при замене подынтегральной функции на константу. В качестве константы можно взять значение функции в любой точке отрезка 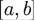 . Наиболее часто используются значения функции в середине отрезка и на его концах. Соответствующие модификации носят названия методов средних прямоугольников, левых прямоугольников и правых прямоугольников.
. Наиболее часто используются значения функции в середине отрезка и на его концах. Соответствующие модификации носят названия методов средних прямоугольников, левых прямоугольников и правых прямоугольников.
По методу средних прямоугольников на интервале [xi,xi+h]имеем
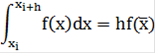
1.2.1 Метод средних прямоугольников для n=1
При n=1:
i=ai+h=b
 =
= 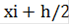
h=(b-a)/n
Исходя из этого получаем уравнение:
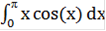 = ((b-a)/n) * (
= ((b-a)/n) * ( cos(
cos( ))
))
Подставляя в полученное уравнение исходные данные получаем:
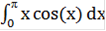 =((
=(( - 0)/1)*((0+((
- 0)/1)*((0+(( - 0)/1)/2)*cos(0+((
- 0)/1)/2)*cos(0+(( - 0)/1)/2)) = 0
- 0)/1)/2)) = 0
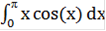 = 0
= 0
Погрешность:
R= 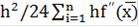 =-2,584
=-2,584
1.2.2 Метод средних прямоугольников для n=2
В данном случае исходный отрезок интегрирования разбивается на 2 отрезка интегрирования: (0; 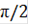 ) и (
) и (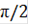 ;
; 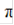 ).
).
В связи с этим:
X1=0
X2= 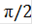
 =
= 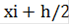
h=(b-a)/n
По полученным данным получаем уравнение:
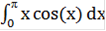 = ((b-a)/2)*(((x1+(b-a)/4)*(cos(x1+(b-a)/4))+((x2+(b-a)/4)*
= ((b-a)/2)*(((x1+(b-a)/4)*(cos(x1+(b-a)/4))+((x2+(b-a)/4)*
*(cos(x2+(b-a)/4))
Подставляем в полученное уравнение начальные данные и получаем:
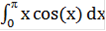 = ((
= (( -0)/2)*(((0+(
-0)/2)*(((0+(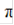 -0)/4)*(cos(0+(
-0)/4)*(cos(0+(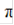 -0)/4))+(
-0)/4))+( (
(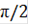 +(
+(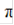 -
-
)/4)* *(cos(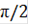 + (
+ ( -0)/4)) = -1,745
-0)/4)) = -1,745
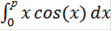 = -1,745
= -1,745
Погрешность:
R= 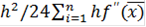 =-0,636
=-0,636
1. 3 Метод трапеций
Метод трапеций - метод численного интегрирования <http://ru.wikipedia.org/wiki/%D0%A7%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%BD%D0%BE%D0%B5_%D0%B8%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5> функции одной переменной, заключающийся в замене на каждом элементарном отрезке подинтегральной функции на многочлен первой степени, то есть линейную функцию.
Если отрезок (xi;xi+h) является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле
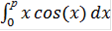 =
= 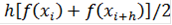
. 1 Метод трапеций при n=1
На отрезке (a;b) заменяем f(x) полином первой степени.
В этом случае
Xi=a
Xi+h=b
h=(b-a)/n
и уравнение имеет вид:
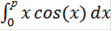 = ((b-a)/n)*[(a cos(a))+(b cos(b))]/2
= ((b-a)/n)*[(a cos(a))+(b cos(b))]/2
Подставим исходные данные и получим:
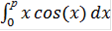 = ((
= (( -0)/1)*[(0 * cos(0))+(
-0)/1)*[(0 * cos(0))+( *cos(
*cos(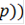 ]/2 = -4,935
]/2 = -4,935
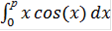 = -4,935
= -4,935
Погрешность:
R0=(-h3/12)*f’’’(xi)= 8,117
1.3.2 Метод трапеций при n=2
Отрезке (a;b) разбиваем на 2 отрезка (a;c) и (c;b) и замеим f(x) полином первой степени на обоих отрезках.
В этом случае
X1=a
X2 =c = (a+b)/2
X3 =b
h=(b-a)/n
и уравнение имеет вид:
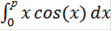 = ((b-a)/n)*(([(a cos(a))+(c cos(c))]/2)+([(c cos(c))+(b (b))]/2))
= ((b-a)/n)*(([(a cos(a))+(c cos(c))]/2)+([(c cos(c))+(b (b))]/2))
Подставим исходные данные и получим:
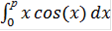 = ((
= (( -0)/1)*(([(0 * cos(0))+(
-0)/1)*(([(0 * cos(0))+(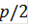 *cos(
*cos(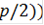 ]/2)+ ([(
]/2)+ ([(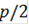 * (
* (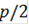 ))+(
))+( * cos(
* cos( ))]/2)) = -2,467
))]/2)) = -2,467
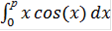 = -2,467
= -2,467
Погрешность:
R0=(-h3/12)*f’’’(xi)=0,646
численный интегрирование симпсон гаусс
Метод Симпсона
Метод Симпсона - метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на полином второй степени, то есть на параболу.
Формула Симпсона:
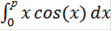 = h[f(x0)+4f(x1)+f(x2)]/3
= h[f(x0)+4f(x1)+f(x2)]/3
Метод Симпсона при n =1
Подынтегральную функцию f(x) заменим полином второй степени P2(x) - параболой, проходящей через равноотстоящие точки x0,x1,x2.
В данном случае
X0=a
X1=c = (a+b)/2
X2 = b
H = (b-a)/2n
Полученное уравнение имеет вид:
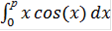 = (b-a)/2n [(a cos(a))+(c cos(c))+(b cos (b))]/3
= (b-a)/2n [(a cos(a))+(c cos(c))+(b cos (b))]/3
Подставляем исходные данные и получаем:
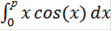 = (
= ( -0)/2*1 [(0 cos(0))+(
-0)/2*1 [(0 cos(0))+(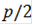 cos(
cos(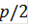 ))+(
))+(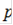 cos (
cos ( ))]/3 = -
))]/3 = -
1,645
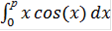 =-1,645
=-1,645
1.4.2 Метод Симпсона при n=2
В данном случае исходный отрезок [a;b] разбиваем на 2: [a;c] и [c;b].
Подынтегральную функцию f(x) заменим полином второй степени P2(x) - параболой, проходящей через равноотстоящие точки x0,x1,x2 - на первом отрезке и x2,x3,x4 - на втором отрезке.
В данном случае
X0=a
X1=d = (a+c)/2
X2 = с= (a+b)/23 = e = (c+b)/24 =b=(b-a)/2n
Полученное уравнение имеет вид:
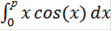 = (b-a)/2n(([(a cos(a))+(d cos(d))+(c cos (c))]/3)+([(c
= (b-a)/2n(([(a cos(a))+(d cos(d))+(c cos (c))]/3)+([(c
cos(c)) + 4(e cos(e)) + (b cos(b))]/3))
Подставляем исходные данные и получаем:
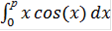 = (
= ( -0)/2*1(([(0 cos(0))+(
-0)/2*1(([(0 cos(0))+(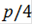 cos(
cos(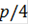 )) + (
)) + (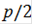 cos (
cos (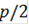
))]/3) + ([(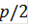 cos (
cos (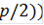 + 4(
+ 4(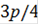 cos(
cos(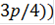 +(
+(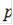 cos (
cos ( )) = -1,986
)) = -1,986
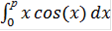 =-1,986
=-1,986
2. Вычисление интеграла 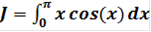 методом Гаусса
методом Гаусса
Метод Гаусса - метод численного интегрирования, позволяющий повысить алгебраический порядок точности методов на основе интерполяционных формул путём специального выбора узлов интегрирования без увеличения числа используемых значений подынтегральной функции. Метод Гаусса позволяет достичь максимальной для данного числа узлов интегрирования алгебраической точности.
Например, для двух узлов можно получить метод 3-го порядка точности, тогда как для равноотстоящих узлов метода выше 2-го порядка получить невозможно. В общем случае, используя 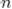 точек, можно получить метод с порядком точности
точек, можно получить метод с порядком точности 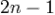 . Значения узлов метода Гаусса по
. Значения узлов метода Гаусса по 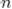 точкам являются корнями полинома Лежандра степени
точкам являются корнями полинома Лежандра степени 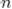 и приводятся в справочниках специальных функций вместе с соответствующими весами.
и приводятся в справочниках специальных функций вместе с соответствующими весами.
Формула:
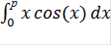 =
= 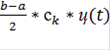
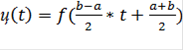 ,
,
Где t- координаты узлов
Ck - весовые коэффициенты
 2020-04-20
2020-04-20 164
164







