2020-04-20
119
При наличии 1-го узла
t=0
ck = 2
Формула имеет вид:
= 
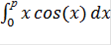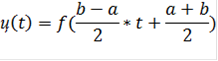
Подставим в данную формулу исходные данные и получим:
= 
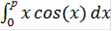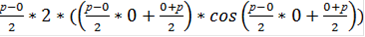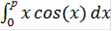=0
=0
Двухточечная схема метода Гаусса
При наличии 2-х узлов
t1=-1/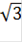 
t2 = 1/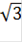
c1 = 1
c2 = 1
Формула имеет вид:
= 
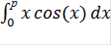Подставим в данную формулу исходные данные и получим:
= 
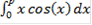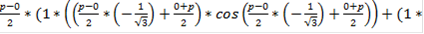
= -2,244
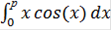=-2,244
Трехточечная схема метода Гаусса
При наличии 3-х узлов
t1= - 
t2 = 0
t3 =
c1 = 5/9
c2 = 8/9
c3 =5/9
Формула имеет вид:
= 
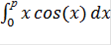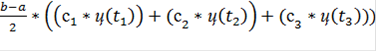
Подставим в данную формулу исходные данные и получим:
= 
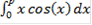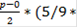
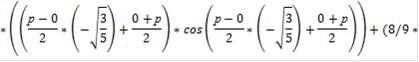
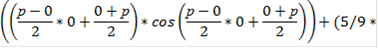
= -1,992
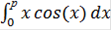=-1,992
Сравнительный анализ точности полученных результатов
| Метод | Точное значение интеграла  =
| Погрешность |
| Аналитически | -2 | - |
| Средних прямоугольников, n=1 | 0 | -2,584 |
| Средних прямоугольников, n=2 | -1,745 | -0,636 |
| Трапеций, n=1 | -4,935 | 8,117 |
| Трапеций, n=2 | -2,467 | 0,646 |
| Симпсона, n=1 | -1,645 | -0,355 |
| Симпсона, n=2 | -1,986 | 0,014 |
| Гаусса, n=1 | 0 | -2 |
| Гаусса, n=2 | -2,244 | 0,244 |
| Гаусса, n=3 | -1,992 | -0,008 |
4. Вычисление интеграла 
Аналитически
Вычислим внутренний интеграл
i=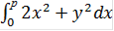 
.
Интеграл суммы равен сумме интегралов, следовательно:
= 
+ 
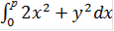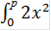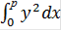= 2* 
+ 
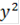x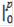 
= (2/3 
+ 
) =
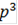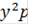,639 + 3,14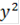
Подставим полученное значение во внешний интеграл и вычислим его.
= 
+ 
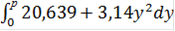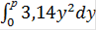=20,639y +
,14 
= 64,807 + 32, 404 = 97,211
4.2 Метод Гаусса.
Двойной интеграл вычисляется методом Гаусса аналогично одномерному случаю.
Одноточечная схема.
При наличии 1-го узла
=0
ci,j = 2
Формула имеет вид:
= 
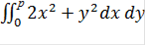Подставим в данную формулу исходные данные и получим:
= 
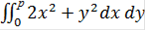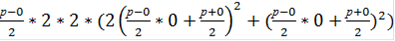
= 46,472
Двухточечная схема
При наличии 2-х узлов
t1=-1/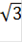 
2 = 1/ 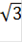1 = 12 = 1
= 
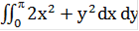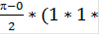
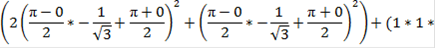
= 31
Вывод:
По проведенным нами расчетам можно сделать вывод о том, что наиболее точными методами численного интегрирования являются метод Симпсона и метод Гаусса при наибольшем количестве разбиений.
