Лекция 1.
I. Кванторы общности и существования. Логическое следствие и логическая равносильность.
Символ 
| означает: | для любого  . .
|
Символ 
| означает: | существует такое  , что. , что.
|
Символ 
| означает: | логическое следствие. |
Символ 
| означает: | логическую равносильность. |
(А) 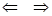 (Б) (Б)
| (Б) является необходимым и достаточным для выполнения (А) |
(А) 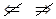 (Б) (Б)
| (Б) является не необходимым и не достаточным для выполнения (А) |
(А)  (Б) (Б)
| (Б) является необходимым, но не достаточным для выполнения (А) |
(А)  (Б) (Б)
| (Б) является не необходимым, но достаточным для выполнения (А) |
II. Множества.
Множество  , состоящее из элементов , состоящее из элементов 
|   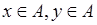 , , 
|
Множество  , состоящее из элементов , состоящее из элементов  , удовлетворяющих условию , удовлетворяющих условию 
| 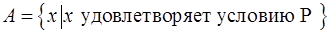
|
 - -
| пустое множество. |
 - -
|  подмножество множества подмножество множества  . .
|
 - -
| множества  и и  совпадают. совпадают.
|
Объединение множеств.
Определение:  ;
;
свойства:
 , ,
|  , ,
| 
|
 , ,
|  , ,
| 
|
Пересечение множеств.
Определение:  ;
;
свойства:
 , ,
|  , ,
| 
|
 , ,
|  , ,
| 
|

| 
|
Разность множеств.
Определение:  ;
;
свойства:
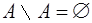 , ,
|  , ,
|
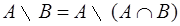 , ,
|  . .
|
Дополнение множества до основного множества  .
.
Определение: 
 ;
;
свойства:
 , ,
|  . .
|
Принцип двойственности.
 , ,
|  . .
|
III. Действительные числа и числовые множества.
Множества
| 1)Натуральных чисел |  , ,
|
| 2)целых чисел |  , ,  , ,
|
| 3)рациональных чисел |  , ,
|
| 4)действительных (вещественных) чисел | 
|
Числовые промежутки
| Отрезок (замкнутый промежуток) |  . . 
|
| Интервал (открытый промежуток) |  . .
|
| Полуинтервалы |  , ,  . .
|
| Бесконечные числовые промежутки (лучи, полупрямые) |  , ,
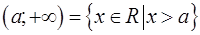 , ,
 , ,
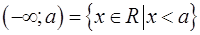 . .
|
 окрестность точки окрестность точки 
| 
|
Правая  окрестность точки окрестность точки 
| 
|
Левая  окрестность точки окрестность точки 
| 
|
Проколотая  окрестность точки окрестность точки 
| 
|
Числовая прямая
 .
.
Абсолютная величина числа

Свойства абсолютной величины числа
1.  ; ;
| 2. 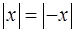 ; ;
| 3.  ; ;
|
4.  ; ;
| 5.  ; ;
| 6.  ; ;
|
7. 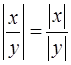 ; ;
| 8.  ; ;
| 9.  ; ;
|
Лекция 2.
Числовые последовательности.
Определение. Пусть каждому числу  натурального ряда чисел
натурального ряда чисел  ставится в соответствие вещественное число
ставится в соответствие вещественное число  . Тогда множество занумерованных вещественных чисел
. Тогда множество занумерованных вещественных чисел  называется числовой последовательностью.
называется числовой последовательностью.
Числа  называются элементами последовательности,
называются элементами последовательности,  - общим членом последовательности.
- общим членом последовательности.
Обозначение  - последовательность чисел
- последовательность чисел  .
.
Действия над последовательностями.
 , ,
|  , ,
|
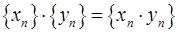 , ,
| 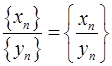 , ,  ,при ,при  . .
|
Ограниченные и неограниченные последовательности.
Последовательность  называется ограниченной сверху называется ограниченной сверху
| 
| 
|
Последовательность  называется ограниченной снизу называется ограниченной снизу
| 
| 
|
Последовательность  называется ограниченной называется ограниченной
| 
| 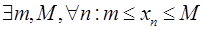
|
Последовательность  называется неограниченной называется неограниченной
| 
| 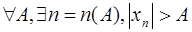
|
 2020-04-20
2020-04-20 174
174







