Вычисление ранга матрицы методом окаймляющих маноров

Векторная алгебра и анализ

2.1. Определители, матрицы, системы линейных уравнений

Автор Л.Ю. Трояновская.

Лекция 3. Ранг матрицы, обращение матриц.

Содержание:

1. Ранг матрицы. ♦
2. Вычисление ранга матрицы методом окаймляющих маноров. ♦
3. Вычисление ранга матрицы методом элементарных преобразований. ♦
4. Обратная матрица. ♦
5. Вычисление обратной матрицы методом присоединенной матрицы. ♦
6. Вычисление обратной матрицы методом элементарных преобразований. ♦
7. Решение матричных уравнений. ♦

Ранг матрицы.

Выберем в матрице  размером  одинаковое число строк и столбцов, равное , где .

Определение 1. Элементы, стоящие на пересечении выбранных  строк и столбцов в матрице  размером  образуют квадратную матрицу порядка , определитель которой называется минором  - го порядка матрицы .

Пример.

размер этой матрицы , значит возможные значения  – 1, 2 или 3.

. Миноров первого порядка ровно столько, сколько элементов в матрице, т.е. 15. Например, выберем вторую строчку и третий столбец. На их пересечении стоит один элемент , значит, .

. Выберем, например, первую и третью строки, второй и пятый столбцы. На их пересечении стоят четыре элемента: , значит, .

. Строки мы можем выбрать только первую, вторую и третью, т.к. других нет. А вот три столбца из пяти можно выбрать произвольно. Например, первый, третий и пятый. Тогда минор третьего порядка будет .

Миноров большего порядка в этой матрице нет, т.к. минор соответствует квадратной таблице, а максимальный квадрат в этой матрице – три на три. Минор – это определитель, т.е. число, которое может равняться нулю или быть ненулевым.

Определение 2. Минор матрицы называется базисным, если он не равен нулю, а миноры большего порядка не существуют или все равны нулю.

В предыдущем примере минор третьего порядка является базисным, т.к. он не равен нулю, а миноров большего порядка не существует. В этой матрице любой ненулевой минор третьего порядка можно назвать базисным.

Определение 3. Порядок базисного минора называется рангом матрицы.

Обозначение:  или просто .

В предыдущем примере порядок базисного минора равен трем, значит ранг матрицы равен трем, т.е. .

Вычисление ранга матрицы методом окаймляющих маноров.

Если в матрице выбрать минор п – го порядка, то окаймляющим для него будет любой минор (п+ 1) – го порядка, содержащий исходный минор целиком. Т.е., к выбранным строкам и столбцам мы добавляем еще одну строку и один столбец.

Пример.

 .

Выберем любой ненулевой элемент, например,  тогда  этот минор можно окаймить.

.

Добавим к выбранным первому столбцу и первой строке вторую строку и второй столбец:

 

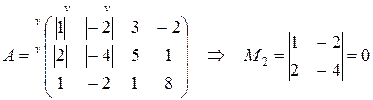, но у  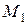есть другие окаймляющие миноры. Например, вместо второго столбца добавим третий:

 этот минор можно окаймить. Строку можно добавить только третью, а столбцы – второй или четвертый. Следовательно,  у найденного ненулевого минора второго порядка  есть два окаймляющих –  и . Проверим, есть ли среди них ненулевые. Вычислим : к первой и второй строкам добавим третью, а к первому и третьему столбцу добавим второй .

Тогда вычислим : к первой и второй строкам добавим третью, а к первому и третьему столбцу добавим четвертый

. Следовательно, , т.к. есть минор 2-го порядка, не равный нулю, а все окаймляющие его миноры 3-го порядка равны нулю.