Види функцій керування стохастичною системою

ПОСТАНОВКА ЗАДАЧІ ОПТИМАЛЬНОГО СТОХАСТИЧнОГО КЕРУВАННЯ

Загальні положення

 

Позначатимемо 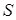 – простір станів, , .

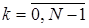Можливі керування є множиною припустимих керувань , яка у свою чергу є підмножиною простору керувань : , .

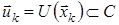Послідовність керуючих функцій 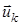, , записана у вигляді

 (1),

 

називається стратегією керування.

Задача оптимального керування системою (1) полягає в пошуку такої послідовності функцій керування 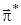, що мінімізує цільовий функціонал системи за  кроків. Ця послідовність 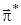 називається оптимальною стратегією керування.

Визначення. Якщо кількість кроків, на яких досліджується поведінка системи, є скінченною, то задача називається задачею зі скінченним горизонтом рішення. Якщо ж ми розв’язуємо задачу на нескінченному часовому інтервалі (), то горизонт рішення є нескінченним.

Задача оптимального стохастичного керування з дискретним часом випливає із детермінованої задачі, якщо система функціонує за умов випадкових збурень 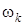. У цьому випадку функція (1), що визначає стан системи на кожному наступному кроці, залежить від поточного стану , керування 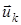 і випадкових збурень :

 

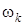, .                           (2)

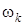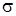Збурення  є елементами деякого ймовірнісного простору  (де  – простір збурень,  – -алгебра підмножин з ) і має розподіл .

Критерії якості

 

Розглянемо спочатку критерії якості, які найчастіше використовуються в детермінованих дискретних задачах керування, а потім перейдемо до стохастичного випадку. Якщо на кожному кроці функціонування системи задана функція , що визначає витрати за один крок керування, то критерій якості руху матиме вигляд

 

.                             (3)

 

Величина , що називається коефіцієнтом дисконтування, визначає внесок витрат за всі попередні кроки на кожному поточному кроці.

Найчастіше критерій (3) використовується в тих випадках, коли необхідно розв’язувати задачі, пов'язані з витратами деяких видів ресурсів. Саме цей функціонал ми будемо використовувати надалі.

Крім критерію (3) розглядаються також критерії, які мінімізують горизонт системи  і є аналогом часу руху для неперервних систем. У цьому випадку цільовий функціонал матиме вигляд

 

.

 

Також часто в дискретних задачах керування використовуються термінальні функціонали якості

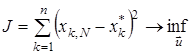 або ,

 

де  – заданий стан системи,  – кінцевий стан системи.

Оскільки в задачі оптимального стохастичного керування збурення  випадкові, то може бути тільки апріорна інформація про них, наприклад, у вигляді функції розподілу, відомої повністю або частково. У цьому випадку якість процесу керування оцінюється за допомогою формули

 

,

 

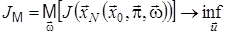яка дорівнює математичному сподіванню функції .

 

Види функцій керування стохастичною системою

 

Задача детермінованого керування відрізняється від свого стохастичного аналога тим, що в першій відсутні неконтрольовані фактори 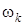, і еволюція системи однозначно визначається обраним керуванням 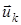. Отже, у задачі детермінованого керування для кожного початкового стану  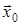можна заздалегідь вибрати послідовність оптимальних керувань , , …, , застосування яких дає оптимальне значення функціонала .

Для стохастичної системи в загальному випадку цього зробити не можна, оскільки система переходить зі стану в стан не тільки під дією керування 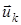; на неї на кожному кроці також впливають випадкові величини 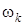. Очевидно, що, по-перше, ці величини можуть так змінити траєкторію системи, що обране раніше за оптимальне керування  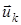в момент його застосування вже таким не буде, і, по-друге, інформація, одержувана на кожному кроці про впливи 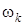, що мали місце, може бути додатково використана для поліпшення якості керування (рис. 1).

 

Рисунок 1 – Еволюція стохастичної системи ( – заданий стан)

 

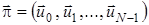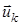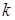Отже, для розв’язання задач оптимального стохастичного керування доцільно використовувати стратегії , у яких  – функція минулих станів системи. У цьому випадку схема визначення оптимального керування на кожному кроці наступна. Якщо  – початковий стан системи, то за перше керування вибирається функція . Якщо мали місце стани , …,  і були задані керування , …, , то керування на -му кроці вибирається як функція 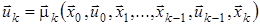, ( для всіх 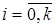). Отже, для вибору керування використовується вся інформація, що є в наявності. Описана стратегія керування є позиційною, оскільки керування визначається залежно від реалізованих позицій (станів) системи, на відміну від програмного керування, коли послідовність керувань визначається заздалегідь, до початку процесу керування, і є функцією часу.

Розглянемо окремі випадки.

Якщо , , то керування називається стаціонарним керуванням. Такі стратегії найпростіші, оскільки є одним і тим же вектором для всіх моментів часу.

Керування , , називається марковською позиційною стратегією (стратегією, кожний елемент якої залежить тільки від поточного стану системи).

Керування , , називається напівмарковською позиційною стратегією (стратегією, кожний елемент якої залежить тільки від поточного і початкового станів системи).

Марковські та напівмарковські позиційні стратегії використовуються найчастіше.

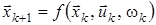Зрозуміло, що в загальному випадку кінцевий стан системи , згідно з формулою (2) , , залежить від початкового стану , керувань 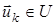 і збурень . Щоб переконатися в цьому, досить виразити в (2)  через , потім  через 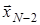 і т.д. Якщо ці перетворення можливо провести, то одержимо співвідношення . Це означає, що різним реалізаціям випадкового збурення  для одного початкового стану  відповідатимуть різні оптимальні стратегії керування .