Сформулюємо задачу оптимального стохастичного керування (4) – (5), а також алгоритм динамічного програмування за допомогою відображення 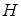 , яке задане формулою:
, яке задане формулою:
 .
.
Розглянемо оператори 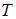 і
і 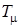 , які відображують множину функцій, що приймають дійсні значення на
, які відображують множину функцій, що приймають дійсні значення на  , в себе:
, в себе:
 ,
,
 ,
, 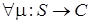 .
.
За таких позначень задачу оптимального стохастичного керування (4) – (5) можна записати у вигляді:
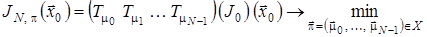 ,
,
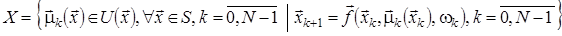 ,
,
де 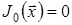 ,
, 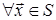 , а
, а 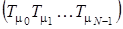 – суперпозиція операторів
– суперпозиція операторів 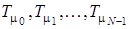 (нагадаємо, що суперпозицією відображень
(нагадаємо, що суперпозицією відображень 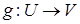 і
і 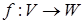 називається відображення
називається відображення 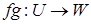 таке, що
таке, що 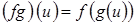 ,
, 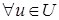 ).
).
Алгоритм динамічного програмування (9) – (10) у термінах відображень можна записати у такий спосіб:
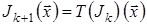 ,
,  ,
,
звідки випливає, що  , де
, де 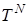 –
– 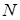 -кратний добуток оператора
-кратний добуток оператора 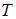 на себе.
на себе.
Задачу з нескінченним горизонтом (6)-(7) у термінах відображень
можна сформулювати в такий спосіб.
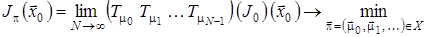 ,
,
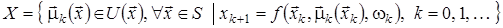 .
.
Функціональне рівняння Беллмана тепер буде еквівалентно рівності
 ,
, 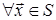 .
.
 2020-04-20
2020-04-20 97
97







