Примеры решения задач

Пример 1. Вычислить интеграл

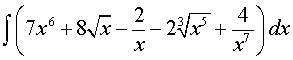
Решение. Воспользовавшись свойствами степеней, а затем правилами интегрирования и формулами из таблицы неопределенных интегралов, получаем

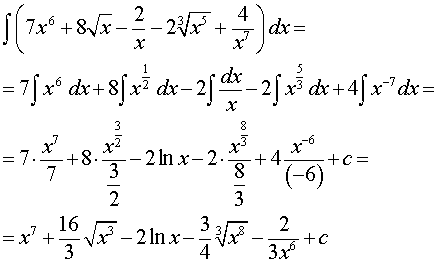
Ответ.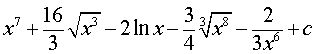

Пример 2. Значение первообразной F (x) функции f (x) = – 4 sin x в точке x = 0 равно 9. Найти .

Решение. Поскольку

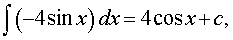
то F (x) = 4 cos x + c,

(6)

Подставляя в формулу (6) значение x = 0, находим значение постоянной интегрирования c:

F (0) = 4 cos 0 + c = 9,

4 + c = 9, c = 5.

Следовательно,

F (x) = 4 cos x + 5

Поэтому

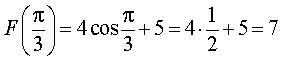
Ответ. 7

Пример 3. Найти первообразную F (x) функции

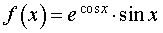
если F (2π) = 2 e + 3.

Решение. Воспользовавшись формулой из таблицы неопределенных интегралов

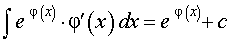
для функции φ (x) = cos x, получаем

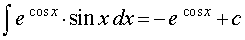
Следовательно,

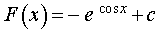
(7)

Подставляя в формулу (7) значение x = 2π, находим значение постоянной интегрирования c:

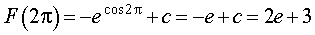
Итак,

c = 3 e +3.

Ответ.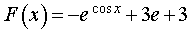

Пример 4. Вычислить интеграл

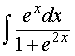
Решение. Воспользовавшись формулой из таблицы неопределенных интегралов

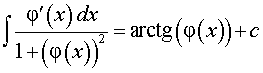
для функции φ (x) = e^x, получаем

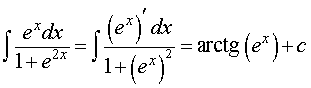
Ответ.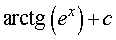

Пример 5. Вычислить интеграл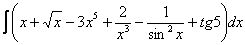

Решение. Применяем правило .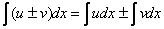

 

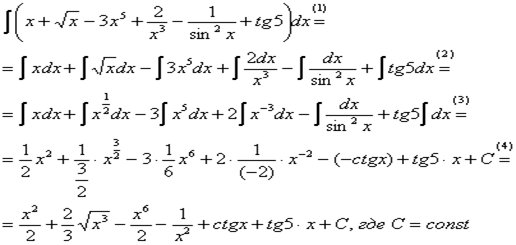
Задания для самостоятельного решения.

Найти неопределенные интегралы

1. ;

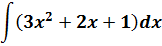2. ;

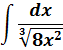3. ;

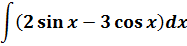4. ;

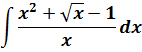5. ;

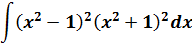6. ;

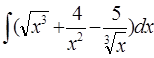7. ;

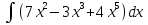8. :

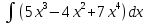9. :

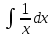10.