Простейшими называются тригонометрические уравнения следующих четырёх видов:
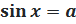
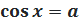
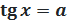
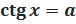
Любое тригонометрическое уравнение в конечном счёте сводится к решению одного или нескольких простейших. Для решения простейших тригонометрических уравнений мы будем пользоваться тригонометрическим кругом и определениями тригонометрических функций.
I. Уравнения 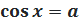 и
и 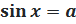
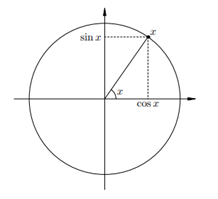 Напомним, что
Напомним, что 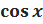 — абсцисса точки на единичной окружности, соответствующей углу x, а
— абсцисса точки на единичной окружности, соответствующей углу x, а 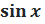 — её ордината.
— её ордината.
Из определения синуса и косинуса следует, что уравнения 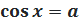 и
и 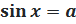 имеют решения только при условии
имеют решения только при условии 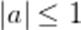 .
.
Помним: Уравнения 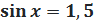 или
или 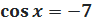 решений не имеют!
решений не имеют!
Начнём с самых простых уравнений.
1. 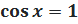 .
.
Мы видим, что на единичной окружности имеется лишь одна точка с абсциссой 1:
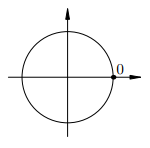 Эта точка соответствует бесконечному множеству углов:
Эта точка соответствует бесконечному множеству углов: 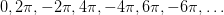 . Все они получаются из нулевого угла прибавлением целого числа полных углов
. Все они получаются из нулевого угла прибавлением целого числа полных углов 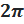 (т. е. нескольких полных оборотов как в одну, так и в другую сторону).
(т. е. нескольких полных оборотов как в одну, так и в другую сторону).
Следовательно, все эти углы могут быть записаны одной формулой:
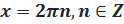 . Это и есть множество решений данного уравнения. Напоминаем, что Z — это множество целых чисел.
. Это и есть множество решений данного уравнения. Напоминаем, что Z — это множество целых чисел.
 2.
2. 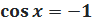
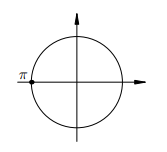
Снова видим, что на единичной окружности есть лишь одна точка с абсциссой — 1:
Эта точка соответствует углу 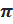 и всем углам, отличающихся от
и всем углам, отличающихся от 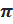 на несколько полных оборотов в обе стороны, т. е. на целое число полных углов. Следовательно, все решения данного уравнения записываются формулой:
на несколько полных оборотов в обе стороны, т. е. на целое число полных углов. Следовательно, все решения данного уравнения записываются формулой: 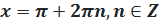
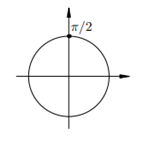 3. 3. 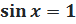 Отмечаем на тригонометрическом круге единственную точку с ординатой 1:
И записываем ответ: Отмечаем на тригонометрическом круге единственную точку с ординатой 1:
И записываем ответ:
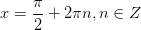
| 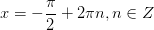  4. 4. 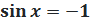 Можете, кстати, записать ответ и в другом виде:
Можете, кстати, записать ответ и в другом виде:
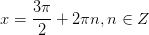
|
Вывод: чтобы описать множество углов, отвечающих одной-единственной точке тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить 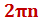 .
.
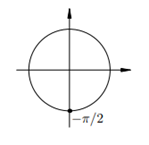
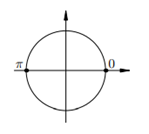 5. 5. 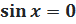 На тригонометрическом круге имеются две точки с ординатой 0. Эти точки соответствуют углам На тригонометрическом круге имеются две точки с ординатой 0. Эти точки соответствуют углам 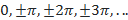 Все эти углы получаются из нулевого угла прибавлением целого числа углов Все эти углы получаются из нулевого угла прибавлением целого числа углов 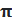 (т. е. с помощью нескольких полуоборотов в обе стороны).И записываем ответ: (т. е. с помощью нескольких полуоборотов в обе стороны).И записываем ответ: 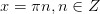
| 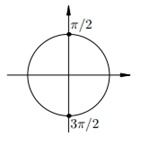 6. 6. 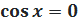 Все углы, отвечающие этим точкам, получаются из Все углы, отвечающие этим точкам, получаются из 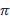 /2 прибавлением целого числа углов /2 прибавлением целого числа углов 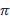 (полуоборотов): (полуоборотов):
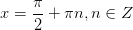
|
Точки, лежащие на концах диаметра тригонометрического круга, мы будем называть диаметральной парой.
Вывод: Чтобы описать множество углов, отвечающих диаметральной паре точек тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить  .
.
II. Переходим к следующему этапу. Теперь в правой части будет стоять табличное значение синуса или косинуса (отличное от 0 или 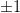 ). Начинаем с косинуса.
). Начинаем с косинуса.
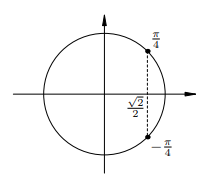
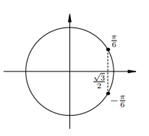
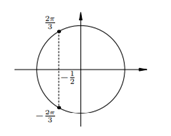
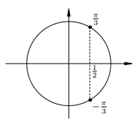 7. 7. 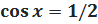 Имеем вертикальную пару точек с абсциссой ½. Все углы, соответствующие верхней точке, описываются формулой Имеем вертикальную пару точек с абсциссой ½. Все углы, соответствующие верхней точке, описываются формулой 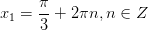 (вспомните первое полезное наблюдение!). Аналогично, все углы, соответствующие нижней точке, описыва-ются формулой: (вспомните первое полезное наблюдение!). Аналогично, все углы, соответствующие нижней точке, описыва-ются формулой: 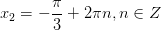 Обе серии решений можно описать одной формулой:
Обе серии решений можно описать одной формулой: 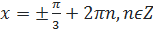
| 8. 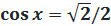
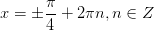
|
9. 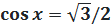
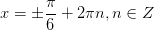 
| 10. 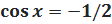
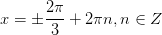 
|
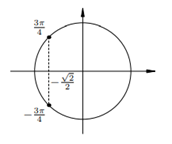 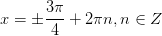 11. 11. 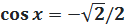
| 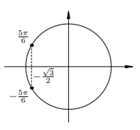 12. 12. 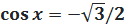
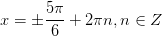
|
III. Уравнение 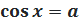
 Уравнение
Уравнение 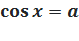 также имеет решения лишь при
также имеет решения лишь при 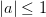 . Случай
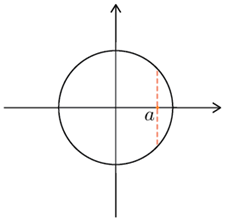
. Случай 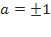 рассмотрен выше. Решения уравнения
рассмотрен выше. Решения уравнения 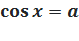 при
при 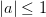 изображаются вертикальной парой точек с абсциссой a:
изображаются вертикальной парой точек с абсциссой a:
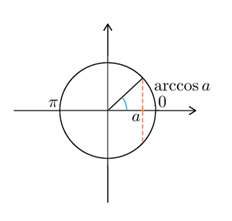
Как вы уже догадались, сейчас возникнет новая функция – арккосинус. Кто лучший кандидат в арккосинусы – верхняя или нижняя точка? Принципиальной разницы нет, но люди выбрали верхнюю. «Арккосинусы живут сверху», и не просто сверху, а на отрезке 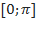 .
.
Арккосинусом числа a называется угол 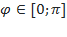 , такой, что
, такой, что 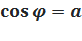 .
.
Обозначение: 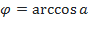 . Область определения арккосинуса – отрезок [-1; 1]. Область значений –отрезок
. Область определения арккосинуса – отрезок [-1; 1]. Область значений –отрезок 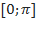 .
.
Промежуток 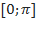 выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно единственное значение угла из промежутка
выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно единственное значение угла из промежутка 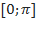 .
.
 Например:
Например:
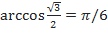 , так как
, так как  и
и 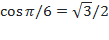
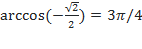 , так как
, так как 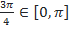 и
и 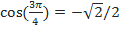
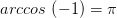
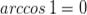
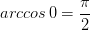
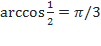
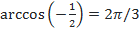
Теперь мы можем решить уравнение 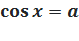 для произвольного a, удовлетворяющего неравенству
для произвольного a, удовлетворяющего неравенству 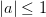 .
.
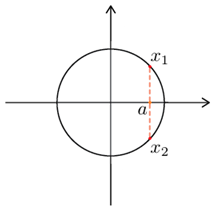 Снова отметим на окружности вертикальную пару точек с абсциссой a. Углы, отвечающие верхней точке, обозначим x1. Углы, отвечающие нижней точке, обозначим x2.
Снова отметим на окружности вертикальную пару точек с абсциссой a. Углы, отвечающие верхней точке, обозначим x1. Углы, отвечающие нижней точке, обозначим x2.
Легко написать формулы для этих углов:
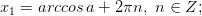
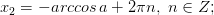
Объединяем их в одну формулу и записываем ответ:
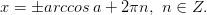
Внимание! Арккосинус не является ни чётной, ни нечётной функцией. Имеет место следующее очевидное соотношение:
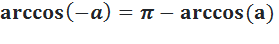
 2020-05-12
2020-05-12 104
104






