Проверим прочность наклонного сечения при действии поперечной силы  (опорная реакция поперечного ребра, см. пункт II.1.2).
(опорная реакция поперечного ребра, см. пункт II.1.2).
Расчёт изгибаемых элементов по наклонному сечению производится из условия:
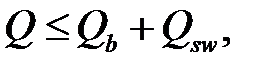 (3.20)
(3.20)
где 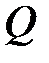 –поперечная сила в конце наклонного сечения с длиной проекции
–поперечная сила в конце наклонного сечения с длиной проекции  на продольную ось элемента, определяемая от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;
на продольную ось элемента, определяемая от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;
 – поперечная сила, воспринимаемая бетоном в наклонном сечении;
– поперечная сила, воспринимаемая бетоном в наклонном сечении;
 – поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении.
– поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении.
1) Поперечная сила  определяется по формуле
определяется по формуле
 , (3.21)
, (3.21)
где  – часть момента, воспринимаемая бетоном:
– часть момента, воспринимаемая бетоном:
 , (3.22)
, (3.22)
где  – коэффициент, учитывающий обжатие и принятый при отсутствии обжатия в поперечном ребре;
– коэффициент, учитывающий обжатие и принятый при отсутствии обжатия в поперечном ребре;
 – расчётное сопротивление бетона растяжению (табл. 2.2 [1]).
– расчётное сопротивление бетона растяжению (табл. 2.2 [1]).
 – длина проекции на горизонтальную ось самой опасной наклонной трещины; при действии на элемент равномерно распределённой нагрузки, невыгоднейшее значение
– длина проекции на горизонтальную ось самой опасной наклонной трещины; при действии на элемент равномерно распределённой нагрузки, невыгоднейшее значение  определяется исходя из знака неравенства:
определяется исходя из знака неравенства:
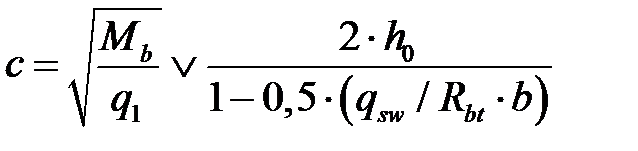 , (3.23)
, (3.23)
где  – условная нагрузка при расчёте наклонных сечений;
– условная нагрузка при расчёте наклонных сечений;
 – усилие в хомутах на единицу длины элемента.
– усилие в хомутах на единицу длины элемента.
Определим условную нагрузку  :
:
– вычислим эквивалентную нагрузку:
 , (3.24)
, (3.24)
где  – полная нагрузка;
– полная нагрузка;
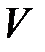 – временная нагрузка (см. табл. 1.2).
– временная нагрузка (см. табл. 1.2).
В данном случае по формуле (3.24) получаем:
 кН/м;
кН/м;
 ,
,
где  – численно равны определённым в пункте II.1.1 величинам
– численно равны определённым в пункте II.1.1 величинам  ;
;
– момент в поперечном ребре от эквивалентных нагрузок (см. формулы (2.3) – (2.5)):

– переходим к условной нагрузке  , которая будет давать такой же момент:
, которая будет давать такой же момент:
 кН/см. (3.25)
кН/см. (3.25)
Вычислим усилие (сопротивление) 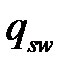 от
от  хомутов на единицу длины элемента:
хомутов на единицу длины элемента:
 . (3.26)
. (3.26)
Для выполнения расчёта по формуле (3.26) необходимо задаться поперечной арматурой.
Из ограничения по сварке, к продольным стержням поперечного ребра  можно приварить стержни диаметром не менее
можно приварить стержни диаметром не менее 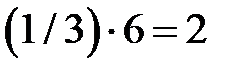 мм, однако, поскольку арматуру диаметром менее 3 мм не выпускают, принимаем
мм, однако, поскольку арматуру диаметром менее 3 мм не выпускают, принимаем  и тогда
и тогда  .
.
Минимальный шаг поперечной арматуры  , в предположении, что она не требуется по расчёту, принимаем из условия:
, в предположении, что она не требуется по расчёту, принимаем из условия:
 (3.27)
(3.27)
Принимаем шаг  .
.
Расстановка поперечной арматуры в поперечном ребре показана на рис. 3.8.
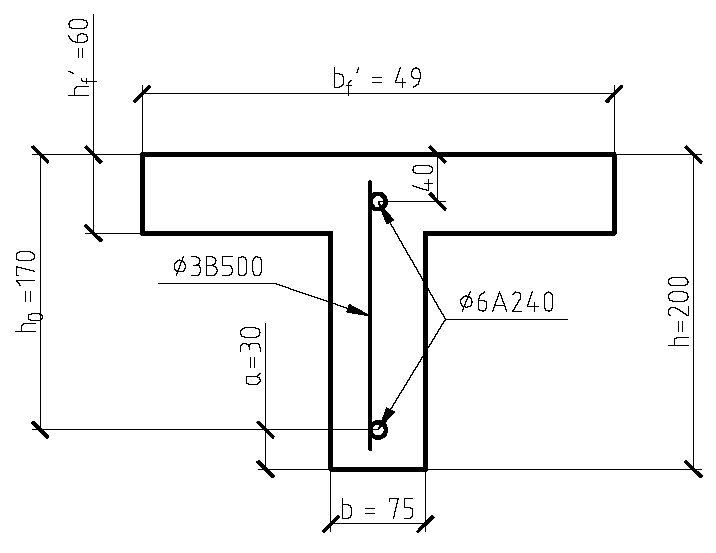
Рис. 3.8. Расстановка поперечной арматуры в сечении поперечного ребра
По формуле (3.26) получаем:
 .
.
Проверим, учитывается ли поперечная арматура в расчёте (по конструктивным условиям она учитывается, если её сопротивление составляет не менее 0,25 сопротивления бетона):
 . (3.28)
. (3.28)
Поперечная арматура в расчёте учитывается.
Теперь можем проверить условие (3.23):
 .
.
Так как левая часть выражения больше правой,  принимаем из условия:
принимаем из условия:
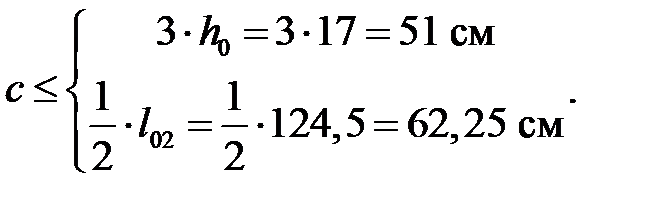 (3.29)
(3.29)
Принимаем  .
.
По формуле (3.21):
 .
.
При этом для  должно выполняться условие:
должно выполняться условие:
 , (3.30)
, (3.30)
где  – минимальная нагрузка, которую может воспринять бетон в любом сечении:
– минимальная нагрузка, которую может воспринять бетон в любом сечении:
 кН. (3.31)
кН. (3.31)
Проверим условие (3.30):
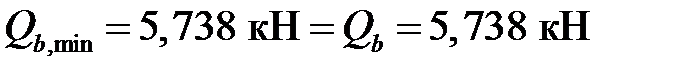 .
.
Равенство в условии (3.30) показывает, что в дальнейшем расчёте можно учитывать как значение  , так и
, так и 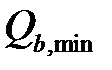 .
.
2) Определим  :
:
 , (3.32)
, (3.32)
где  – принимается из условия:
– принимается из условия:
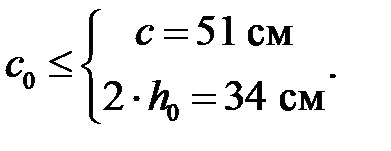 (3.33)
(3.33)
Примем  см.
см.
По формуле (3.32) получим:
 кН.
кН.
3) Определим  – перерезывающую силу, действующую в конце наклонного сечения:
– перерезывающую силу, действующую в конце наклонного сечения:
 кН. (3.34)
кН. (3.34)
4) Проверяем условие прочности наклонного сечения (3.20):
 .
.
Прочность наклонного сечения на действие поперечной силы обеспечена.
 2020-05-12
2020-05-12 223
223








