Преобразованием Лапласа является интегральное преобразование с ядром

а) , где p – комплексная переменная,

б) , где p – комплексная переменная,

в) , где p – комплексная переменная.

31. Изображение второй производной некоторой функции  имеет вид

а) ,   

б) ,        

в) .

32. Если , то для любого постоянного  изображением оригинала  является ;

а) по теореме запаздывания,

б) по теореме подобия,

в) по теореме Ващенко-Захарченко

33. Изображение функции  есть

а)

б)

в) .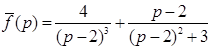

34. Функция  является оригиналом для изображения:

а) ;          

б) ;    

в)  .

35. Если изображение , то оригинал

а)                

б)        

в) .