1. Правило подстановки формулы F вместо переменной x.
2. Правило замены подформул. Если какая–либо формула F, описывающая функцию f, содержит  в качестве подформулы, то замена
в качестве подформулы, то замена  на эквивалентную
на эквивалентную  (
( =
=  ) не изменит функции f; полученная при такой замене новая формула F¢ эквивалентна исходной F.
) не изменит функции f; полученная при такой замене новая формула F¢ эквивалентна исходной F.
Эквивалентные преобразования – преобразования, использующие эквивалентные соотношения и правило замены.
Основные эквивалентные соотношения (законы) в булевой алгебре:
1. Ассоциативность:
а)  ×(
×( ×
×  )
)  (
( ×
×  )×
)× 

 ×
×  ×
×  ;
;
б) 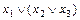



 .
.
2. Коммутативность:
а)  ×
× 

 ×
×  ; б)
; б) 

 .
.
3. Дистрибутивность:
а)  ×(
×( )
) 
 ×
×  ×
×  ; б)
; б)  Ú(
Ú( ×
×  )=(
)=( )×(
)×( ).
).
4. Идемпотентность: а) x×x  x; б) x Ú x
x; б) x Ú x  x.
x.
5. Закон двойного отрицания: 
 x.
x.
6. Свойства констант 0 и 1:
а) x ×1  x; б) x Ú 1
x; б) x Ú 1 
 ; в)
; в) 
 1;
1;
г) x ×0  0; д) x Ú 0
0; д) x Ú 0 
 ; е)
; е) 
 0.
0.
7. Законы де Моргана:

 а)
а) 

 ×
×  ; б)
; б)  ×
× 

 .
.
8. Закон противоречия: x × 
 0.
0.
9. Закон исключенного третьего: 
 1.
1.
Другие соотношения, часто применяемые в преобразованиях булевых формул, выводимы с помощью основных законов. Рассмотрим некоторые задачи эквивалентных преобразований в булевой алгебре и способы их решения.
1. Упрощение формул. Для упрощения формул используются следующие эквивалентные соотношения, выводимые из основных с помощью эквивалентных преобразований:
а) x Ú x × y  x, б) x ×(x Ú y)
x, б) x ×(x Ú y)  x – поглощение; (10)
x – поглощение; (10)
x × y Ú x × 
 x – склеивание; (11)
x – склеивание; (11)
x ×z Ú y × 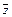 Ú x × y
Ú x × y  x ×z Ú y ×
x ×z Ú y × 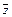 – обобщенное склеивание; (12)
– обобщенное склеивание; (12)
 × y
× y  x Ú y. (13)
x Ú y. (13)
 2020-05-12
2020-05-12 170
170








